
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.
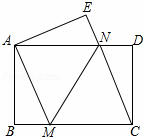
(1)证明:由折叠的性质可得:∠ANM=∠CNM.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠ANM=∠CMN,
∴∠CMN=∠CNM,
∴CM=CN;
(2)解:过点N作NH⊥BC于点H,则四边形NHCD是矩形.
∴HC=DN,NH=DC.
∵△CMN的面积与△CDN的面积比为3:1,
∴MC=3ND=3HC.
∴MH=2HC.
设DN=x,则HC=x,MH=2x,
∴CM=3x=CN,
在Rt△CDN中,CD=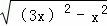 =2
=2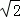 x=4,
x=4,
∴x=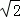 .
.
∴MH=2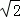 .
.
在Rt△MNH中,MN=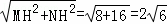 .
.
点评: 此题考查了矩形的性质、折叠的性质、勾股定理以及三角形的面积.此题难度适中,注意掌握辅助线的作法,掌握数形结合思想与方程思想的应用.


科目:初中数学 来源: 题型:
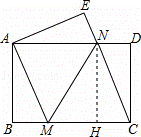
如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
题设(已知): .
结论(求证): .
证明: 省略 .
查看答案和解析>>
科目:初中数学 来源: 题型:
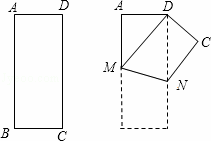
如图,将矩形ABCD沿MN折叠,使点B与点D重合.
(1)求证:DM=DN;
(2)当AB和AD满足什么数量关系时,△DMN是等边三角形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
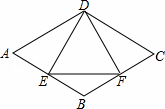
A. 3 B.4 C.1 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com