
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����3��0������0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD�����߶�OP�ӳ�����ȡ��E��ʹPE=AO�����P�˶���ʱ��Ϊt�룮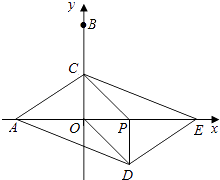
��1������C�˶����߶�OB���е�ʱ����t��ֵ����E�����ꣻ
��2������C���߶�OB��ʱ����֤���ı���ADECΪƽ���ı��Σ�
��3�����߶�PE��ȡ��F��ʹPF=1������F��MN��PE����ȡFM=2��FN=1���ҵ�M��N�ֱ���һ�������ޣ����˶������У���PCOD�����ΪS��
�ٵ���M��N����һ�������ı���ADEC�ı���ʱ�������������������t��ֵ��
������M��N��ǡ��ֻ��һ���������ı���ADEC���ڲ����������߽磩ʱ��ֱ��д��S��ȡֵ��Χ��
���𰸡�
��1��
�⣺��OB=6��C��OB���е㣬
��BC= ![]() OB=3��
OB=3��
��2t=3��t= ![]() ��
��
��OE= ![]() +3=
+3= ![]() ��E��
��E�� ![]() ��0��
��0��
��2��
�⣺��ͼ������CD��OP�ڵ�G��
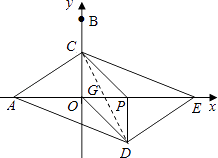
��PCOD��CG=DG��OG=PG��
��AO=PE��
��AG=EG��
���ı���ADEC��ƽ���ı��Σ�
��3��
�⣺�٣�����C��BO��ʱ��
��һ���������ͼ������M��CE����ʱ��
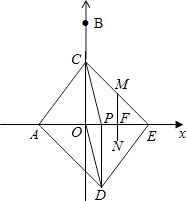
��MF��OC��
���EMF�ס�ECO��
�� ![]() ����
���� ![]() =
= ![]() ��
��
��t=1��
�ڶ������������N��DE��ʱ��
��NF��PD��
���EFN�ס�EPD��
�� ![]() ����
���� ![]() =
= ![]() ��
��
��t= ![]() ��
��
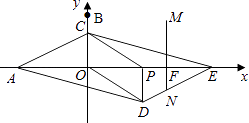
������C��BO���ӳ�����ʱ��
��һ�����������M��DE����ʱ��
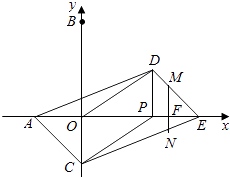
��MF��PD��
���EMF�ס�EDP��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��t= ![]() ��
��
�ڶ������������N��CE����ʱ��
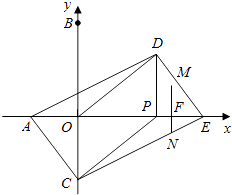
��NF��OC��
���EFN�ס�EOC��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��t=5��
�� ![]() ��S��
��S�� ![]() ��
�� ![]() ��S��20��
��S��20��
��1��t�� ![]() ʱ��
ʱ��
S=t��6��2t��=��2��t�� ![]() ��2+
��2+ ![]() ��
��
��t= ![]() ��1��t��
��1��t�� ![]() ��Χ�ڣ�
��Χ�ڣ�
�� ![]() ��S��
��S�� ![]() ��
��
�� ![]() ��t��5ʱ��S=t��2t��6��=2��t��
��t��5ʱ��S=t��2t��6��=2��t�� ![]() ��2��
��2�� ![]() ��
��
�� ![]() ��S��20��
��S��20��
����������1����C��OB���е����ʱ�䣬�������E�����꣬��2������CD��OP�ڵ�G����PCOD�ĶԽ�����ȣ����ı���ADEC��ƽ���ı��Σ���3������C��BO��ʱ����һ�����������M��CE����ʱ���ɡ�EMF�ס�ECO��⣬�ڶ������������N��DE����ʱ���ɡ�EFN�ס�EPD��⣻����C��BO���ӳ�����ʱ����һ�����������M��DE����ʱ����EMF�ס�EDP��⣬�ڶ������������N��CE����ʱ���ɡ�EFN�ס�EOC��⣻�ڵ�1��t�� ![]() ʱ�͵�
ʱ�͵� ![]() ��t��5ʱ���ֱ����S��ȡֵ��Χ��
��t��5ʱ���ֱ����S��ȡֵ��Χ��
�����㾫����������Ĺؼ������������������ε�Ӧ�õ����֪ʶ�����ղ�ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������⣮


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��  �������⣬��ɱ���Ľ��
�������⣬��ɱ���Ľ��
��1���ⲻ��ʽ�٣��� �� �����ǣ� ��
��2���ⲻ��ʽ�ۣ��� ��
��3���Ѳ���ʽ�٣��ں͢۵Ľ⼯�������ϱ�ʾ������ ![]()
��4����ͼ�п����ҳ���������ʽ�⼯�Ĺ������֣��ò���ʽ��Ľ⼯ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�0��3������B��x���ϣ�����AOB�Ƶ�A��ʱ����ת90��õ���AEF����O��B�Ķ�Ӧ��ֱ��ǵ�E��F��
��1������B�������ǣ���4��0��������ͼ�л�����AEF����д����E��F�����꣮
��2������F����x����Ϸ�ʱ����д��һ�����������ĵ�B�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y1=a��x��x1����x��x2����a��0��x1��x2����ͼ����һ�κ���y2=dx+e��d��0����ͼ���ڵ㣨x1 �� 0����������y=y1+y2��ͼ����x�����һ�����㣬�� ��
A.a��x1��x2��=d
B.a��x2��x1��=d
C.a��x1��x2��2=d
D.a��x1+x2��2=d
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬѧ����һ����ϣ����������������г���M�س�����һ����·����ǰ��N�أ�������ʻ��ʱ��Ϊt��h������������֮��ľ���Ϊy��km����y��t�ĺ�����ϵ��ͼ1��ʾ�� ����˼����������ͼ1�IJ�����ȷ��Ϣ�����ȳ���1h���׳���0.5Сʱ����������
�����������ͬѧ����������⣺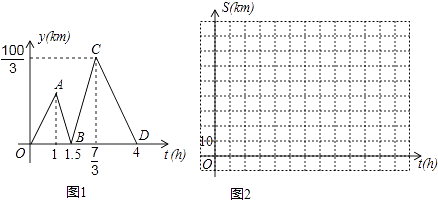
��1���ֱ�����߶�BC��CD����ֱ�ߵĺ�������ʽ��
��2����20��y��30ʱ����t��ȡֵ��Χ��
��3���ֱ�����ף�����ʻ��·��S�� �� S����ʱ��t�ĺ�������ʽ������ͼ2������ֱ������ϵ�зֱ����ǵ�ͼ��
��4������Ħ�г�����ͬʱ��������N����ͬһ��·����ǰ��M�أ��������� ![]() h�����������ʱ����������ʱ�����������
h�����������ʱ����������ʱ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��F��������ABCD�ı�CD�ϵ�һ�����㣬BF�Ĵ�ֱƽ���߽��Խ���AC�ڵ�E������BE��FE�����EBF�Ķ����ǣ� �� 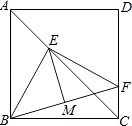
A.45��
B.50��
C.60��
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���о�����ͼ�Σ����������ȸ�������ͼ�εĶ��壬���о��������ʺ��ж��� ���壺�����ڽ���ȵ������νеȽ������Σ�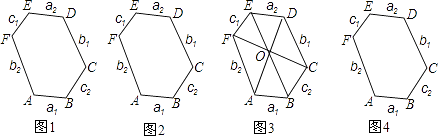
��1���о����� ����ͼ1���Ƚ�������ABCDEF�У��������Ա�AB��DE��BC��EF��CD��AF�ֱ���ʲôλ�ù�ϵ��֤����Ľ��ۣ�
����ͼ2���Ƚ�������ABCDEF�У������AB=DE���������������Ա�BC��EF��CD��AF�����֤����Ľ��ۣ�
����ͼ3���Ƚ�������ABCDEF�У�����������Խ���AD��BE��CF�ཻ��һ��O����ô�������Ա�AB��DE��BC��EF��CD��AF�ֱ���ʲô������ϵ��֤����Ľ��ۣ�
��2��̽���ж� �������Ա߷ֱ�ƽ�е������Σ�������Ҫ�����ڽ�Ϊ120�㣬���ܱ�֤������һ���ǵȽ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��E�DZ�BC�ϵ������㣬��BD=DE=EC������C��CF��AB��AE�ӳ����ڵ�F������FD���ӳ���AB���ڵ�G�� 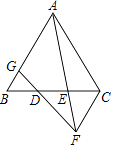
��1����֤��AC=2CF��
��2������AD�������ADG=��B����֤��CD2=ACCF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com