
 如图,直线AC、BD相交于O,△OAB和△OCD都是等腰直角三角形,直线EF过点O,交AD、BC于点E、F,证明下列命题:
如图,直线AC、BD相交于O,△OAB和△OCD都是等腰直角三角形,直线EF过点O,交AD、BC于点E、F,证明下列命题:
|


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
 如图,直角梯形OABC中,AB∥OC,点A坐标为(0,6),点C坐标为(3,0),BC=
如图,直角梯形OABC中,AB∥OC,点A坐标为(0,6),点C坐标为(3,0),BC=| 37 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
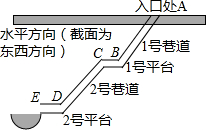 如图是某煤矿地下巷道截面示意图,其中点A为入口,1号巷道与水平地面的夹角为30°,AB长为30米,1号平台BC长为5米,与水平地面平行,2号巷道与水平地面的夹角为45°,CD长为26米,2号平台ED长为8米,与水平地面平行.由于突发透水事故,在2号平台正西方出现险情,水位不断上涨,同时由于2号巷道正上方发生了塌方,阻断了救援人员的营救,被困于2号平台的6名工人面临着严峻的生死考验,事发后,抢险队果断作出决策,在入口A的正西方向某处向地下钻井抽水解救被困工人,根据你所学的知识,确定在距入口A处正西方多远处实施钻井施救较合理,并计算需要钻多深才能抽到水窖中的水?(结果精确到0.1米,参考数据:
如图是某煤矿地下巷道截面示意图,其中点A为入口,1号巷道与水平地面的夹角为30°,AB长为30米,1号平台BC长为5米,与水平地面平行,2号巷道与水平地面的夹角为45°,CD长为26米,2号平台ED长为8米,与水平地面平行.由于突发透水事故,在2号平台正西方出现险情,水位不断上涨,同时由于2号巷道正上方发生了塌方,阻断了救援人员的营救,被困于2号平台的6名工人面临着严峻的生死考验,事发后,抢险队果断作出决策,在入口A的正西方向某处向地下钻井抽水解救被困工人,根据你所学的知识,确定在距入口A处正西方多远处实施钻井施救较合理,并计算需要钻多深才能抽到水窖中的水?(结果精确到0.1米,参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
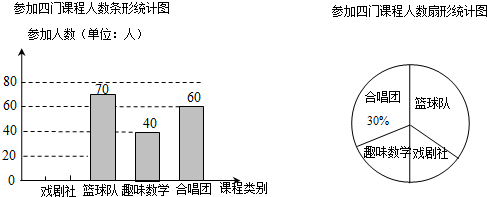
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com