
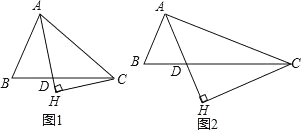
【题目】已知△ABC 中,AD 是∠BAC 的平分线,且 AD=AB,过点 C 作 AD 的垂线,交 AD 的延长线于点 H.
(1)如图 1,若∠BAC=60°.
①直接写出∠B 和∠ACB 的度数;
②若 AB=2,求 AC 和 AH 的长;
(2)如图 2,用等式表示线段 AH 与 AB+AC 之间的数量关系,并证明.
【答案】(1)①45°,②![]() ;(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.证明见解析.
;(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.证明见解析.
【解析】
(1)①先根据角平分线的定义可得∠BAD=∠CAD=30°,由等腰三角形的性质得∠B=75°,最后利用三角形内角和可得∠ACB=45°;②如图 1,作高线 DE,在 Rt△ADE 中,由∠DAC=30°,AB=AD=2 可得 DE=1,AE=![]() , 在 Rt△CDE 中,由∠ACD=45°,DE=1,可得 EC=1,AC=
, 在 Rt△CDE 中,由∠ACD=45°,DE=1,可得 EC=1,AC= ![]() +1,同理可得 AH 的长;(2)如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH,易证△ACH≌△AFH,则 AC=AF,HC=HF, 根据平行线的性质和等腰三角形的性质可得AG=AH,再由线段的和可得结论.
+1,同理可得 AH 的长;(2)如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH,易证△ACH≌△AFH,则 AC=AF,HC=HF, 根据平行线的性质和等腰三角形的性质可得AG=AH,再由线段的和可得结论.
(1)①∵AD 平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∵AB=AD,
∴∠B=![]() =75°,
=75°,
∴∠ACB=180°﹣60°﹣75°=45°;
②如图 1,过 D 作 DE⊥AC 交 AC 于点 E,
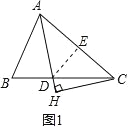
在 Rt△ADE 中,∵∠DAC=30°,AB=AD=2,
∴DE=1,AE=![]() ,
,
在 Rt△CDE 中,∵∠ACD=45°,DE=1,
∴EC=1,
∴AC=![]() +1,
+1,
在 Rt△ACH 中,∵∠DAC=30°,
∴CH=![]() AC=
AC=![]()
∴AH=![]() =
=![]() =
=![]() ;
;
(2)线段 AH 与 AB+AC 之间的数量关系:2AH=AB+AC.
证明:如图 2,延长 AB 和 CH 交于点 F,取 BF 的中点 G,连接 GH.
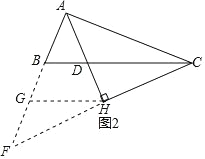
易证△ACH≌△AFH,
∴AC=AF,HC=HF,
∴GH∥BC,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠AGH=∠AHG,
∴AG=AH,
∴AB+AC=AB+AF=2AB+BF=2(AB+BG)=2AG=2AH.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学计划为学校科技活动小组购买![]() 型、
型、![]() 型两种型号的放大镜.若购买8个
型两种型号的放大镜.若购买8个![]() 型放大镜和5个
型放大镜和5个![]() 型放大镜需用235元,购买4个
型放大镜需用235元,购买4个![]() 型放大镜和6个
型放大镜和6个![]() 型放大镜需用170元.
型放大镜需用170元.
(1)求每个![]() 型放大镜和每个
型放大镜和每个![]() 型故大镜各多少元?
型故大镜各多少元?
(2)该中学决定购买![]() 型放大镜和
型放大镜和![]() 型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个
型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个![]() 型放大镜?
型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程(千米)与时间(分)的关系的图象,根据图象信息,下列说法正确的是( )

A. 小王去时的速度大于回家的速度B. 小王在朋友家停留了10分钟
C. 小王去时所花时间少于回家所花时间D. 小王去时走上坡路施,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,AB 的垂直平分线交 AB 于点 D,交 CA 的延长线于点 E,∠EBC=42°,则 ∠BAC=( )

A. 159° B. 154° C. 152° D. 138°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )
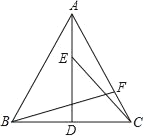
A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价30元![]() 张,暑假为了促销,新推出一种优惠卡:售价300元
张,暑假为了促销,新推出一种优惠卡:售价300元![]() 张,每次凭卡另收15元
张,每次凭卡另收15元![]() 暑假普通票正常出售,优惠卡仅限暑假使用,不限次数
暑假普通票正常出售,优惠卡仅限暑假使用,不限次数![]() 设游泳x次时,所需总费用为y元.
设游泳x次时,所需总费用为y元.
![]() 分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式;
![]() 在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;
在同一坐标系中,若两种消费方式对应的函数图象如图所示,请求出点A、B的坐标;

查看答案和解析>>
科目:初中数学 来源: 题型:
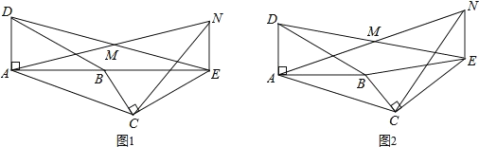
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com