练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某中学计划为学校科技活动小组购买型、型两种型号的放大镜．若购买8个型放大镜和5个型放大镜需用235元，购买4个型放大镜和6个型放大镜需用170元．

    （1）求每个型放大镜和每个型故大镜各多少元？

    （2）该中学决定购买型放大镜和型放大镜共75个，总费用不超过1300元，那么最多可以购买多少个型放大镜？

    【答案】（1）每个型放大镜和每个型放大镜分别为20元，15元；（2）最多可以买35个型放大镜．

    【解析】

    （1）设每个型放大镜和每个型放大镜分别为元，元，列出方程组即可解决问题；

    （2）由题意列出不等式求出即可解决问题．

    （1）设每个型放大镜和每个型放大镜分别为元，元，可得．

    解得：，

    答：每个型放大镜和每个型放大镜分别为20元，15元；

    （2）设购买型放大镜个，根据题意可得：，

    解得：．

    答：最多可以买35个型放大镜．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图, ∠B、∠D的两边分别平行。

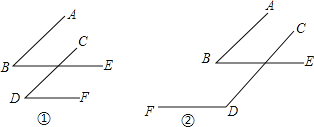
    (1)在图1中，∠B与∠D的数量关系是 ；在图2中，∠B与∠FDC的数量关系是 ；

    (2)用一句话归纳的结论为： ；

    (3)已知∠α的两边与∠β的两边分别平行，并且∠α比∠β的3倍少，求∠α、∠β的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图1，抛物线y=﹣x2﹣x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，﹣1），连接BC、AC

    （1）求出直线AD的解析式；

    （2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；

    （3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：

    成绩x/分

    频数

    频率

    50≤x＜60

    10

    0.05

    　60≤x＜70

    30

    0.15

    　70≤x＜80

    40

    n

    　80≤x＜90

    m

    0.35

    　90≤x≤100

    50

    0.25

    请根据所给信息，解答下列问题：

    (1)m＝　 　，n＝　 　；

    (2)请补全频数分布直方图；

    (3)若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠BAC=90°，AH⊥BC于点H，过点C作CD⊥AC，连接AD，点M为AC上一点，且AM=CD，连接BM交AH于点N，交AD于点E．

    （1）若AB=3，AD=，求△BMC的面积；

    （2）点E为AD的中点时，求证：AD=BN ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中， ，点在边上移动（点不与点， 重合），满足，且点、分别在边、上．

    （）求证： ．

    （）当点移动到的中点时，求证： 平分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

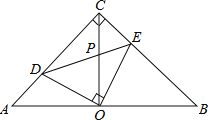
    【题目】如图，在等腰直角△ABC中，∠ACB=90°，O是斜边AB的中点，点D，E分别在直角边AC，BC上，且∠DOE=90°，DE交OC于点P．则下列结论：(1)AD+BE=AC；(2)AD2+BE2=DE2；(3)△ABC的面积等于四边形CDOE面积的2倍；(4)OD=OE．其中正确的结论有( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解

    如图1，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数．

    （1）阅读并补充下面推理过程

    解：过点A作ED∥BC

    ∴∠B=∠　 　，∠C=∠　 　．

    又∵∠EAB+∠BAC+∠DAC=180°（平角定义）

    ∴∠B+∠BAC+∠C=180°

    从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决

    （2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．

    小明受到启发，过点C作CF∥AB如图所示，请你帮助小明完成解答：

    （3）已知AB∥CD，点C在点D的右侧，∠ADC=70°．BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．

    ①如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为　 　°．

    ②如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为　 　°（用含n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

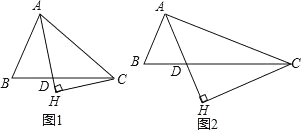
    【题目】已知△ABC 中，AD 是∠BAC 的平分线，且 AD=AB，过点 C 作 AD 的垂线，交 AD 的延长线于点 H．

    （1）如图 1，若∠BAC=60°．

    ①直接写出∠B 和∠ACB 的度数；

    ②若 AB=2，求 AC 和 AH 的长；

    （2）如图 2，用等式表示线段 AH 与 AB+AC 之间的数量关系，并证明．

    查看答案和解析>>

    同步练习册答案