
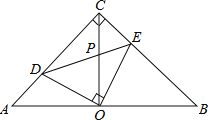
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由等腰直角三角形的性质可得AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO,由“ASA”可证△ADO≌△CEO,△CDO≌△BEO,由全等三角形的性质可依次判断.
∵在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,
∴AC=BC,CO=AO=BO,∠ACO=∠BCO=∠A=∠B=45°,CO⊥AO
∵∠DOE=90°,
∴∠COD+∠COE=90°,且∠AOD+∠COD=90°
∴∠COE=∠AOD,且AO=CO,∠A=∠ACO=45°,
∴△ADO≌△CEO(ASA)
∴AD=CE,OD=OE,故④正确,
同理可得:△CDO≌△BEO
∴CD=BE,
∴AC=AD+CD=AD+BE,故①正确,
在Rt△CDE中,CD2+CE2=DE2,
∴AD2+BE2=DE2,故②正确,
∵△ADO≌△CEO,△CDO≌△BEO
∴S△ADO=S△CEO,S△CDO=S△BEO,
∴△ABC的面积等于四边形CDOE面积的2倍;故③正确,
综上所述:正确的结论有①②③④,
故选D.


科目:初中数学 来源: 题型:
【题目】△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠DCA的平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划为学校科技活动小组购买![]() 型、
型、![]() 型两种型号的放大镜.若购买8个
型两种型号的放大镜.若购买8个![]() 型放大镜和5个
型放大镜和5个![]() 型放大镜需用235元,购买4个
型放大镜需用235元,购买4个![]() 型放大镜和6个
型放大镜和6个![]() 型放大镜需用170元.
型放大镜需用170元.
(1)求每个![]() 型放大镜和每个
型放大镜和每个![]() 型故大镜各多少元?
型故大镜各多少元?
(2)该中学决定购买![]() 型放大镜和
型放大镜和![]() 型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个
型放大镜共75个,总费用不超过1300元,那么最多可以购买多少个![]() 型放大镜?
型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿着BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程(千米)与时间(分)的关系的图象,根据图象信息,下列说法正确的是( )

A. 小王去时的速度大于回家的速度B. 小王在朋友家停留了10分钟
C. 小王去时所花时间少于回家所花时间D. 小王去时走上坡路施,回家时走下坡路
查看答案和解析>>
科目:初中数学 来源: 题型:
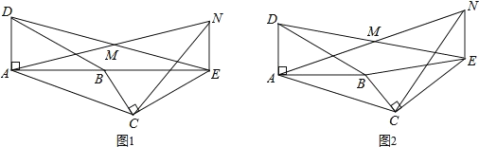
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com