练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动,如果同时出发,则过3s时,△BPQ的面积为____cm2.

    【答案】18

    【解析】

    首先设AB为3xcm，BC为4xcm，AC为5xcm，利用方程求出三角形的三边，由勾股定理的逆定理得出三角形为直角三角形．再求出3秒后的，BP、BQ的长，利用三角形的面积公式计算求解．

    解：设AB为3xcm，BC为4xcm，AC为5xcm，

    ∵周长为36cm，

    AB+BC+AC=36cm，

    ∴3x+4x+5x=36，

    解得x=3，

    ∴AB=9cm，BC=12cm，AC=15cm，

    ∵AB2+BC2=AC2，

    ∴△ABC是直角三角形，

    过3秒时，BP=9-3×1=6（cm），BQ=2×3=6（cm），

    ∴S△PBQ=BPBQ=×（9-3）×6=18（cm2）．

    故答案为：18．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知AM∥BN，∠A=60°，点P是射线AM上一动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．


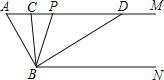
    （1）求∠CBD的度数；
    （2）当点P运动时，∠APB：∠ADB的比值是否随之变化？若不变，请求出这个比值；若变化，请找出变化规律；
    （3）当点P运动到某处时，∠ACB=∠ABD，求此时∠ABC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，解决提出的问题：

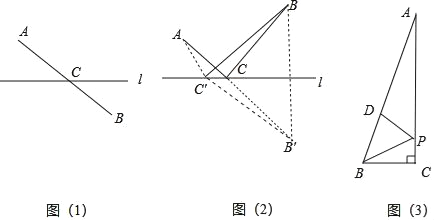
    最短路径问题:如图（1），点A，B分别是直线l异侧的两个点，如何在直线l上找到一个点C，使得点C到点A，点B的距离和最短？我们只需连接AB，与直线l相交于一点，可知这个交点即为所求．

    如图（2），如果点A，B分别是直线l同侧的两个点，如何在l上找到一个点C，使得这个点到点A、点B的距离和最短？我们可以利用轴对称的性质，作出点B关于的对称点B，这时对于直线l上的任一点C，都保持CB＝CB，从而把问题（2）变为问题（1）．因此，线段AB与直线l的交点C的位置即为所求．

    为了说明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′．因为AB′≤AC′+C′B′，∴AC+CB＜AC'+C′B，即AC+BC最小．

    任务：

    数学思考

    （1）材料中划线部分的依据是　 　．

    （2）材料中解决图（2）所示问题体现的数学思想是　 　．（填字母代号即可）

    A．转化思想

    B．分类讨论思想

    C．整体思想

    迁移应用

    （3）如图，在Rt△ABC中，∠C＝90°，∠BAC＝15°，点P为C边上的动点，点D为AB边上的动点，若AB＝8cm，则BP+DP的最小值为　 　cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李师傅负责修理我校课桌椅，现知道李师傅修理2张课桌和3把椅子共需86分钟，修理5张课桌和2把椅子共需149分钟．

    （1）请问李师傅修理1张课桌和1把椅子各需多少分钟

    （2）现我校有12张课桌和14把椅子需要修理，要求1天做完，李师傅每天工作8小时，请问李师傅能在上班时间内修完吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连结CQ.若PA∶PB∶PC=3∶4∶5，连结PQ，试判断△PQC的形状（ ）

    A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上有A、B、C、D四个整数点即各点均表示整数，且，若A、D两点表示的数的分别为和6，点E为BD的中点，那么该数轴上上述五个点所表示的整数中，离线段BD的中点最近的整数是　　

    A. B. 0C. 1D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个由若干小正方形堆成的几何体，它从正面看和从左面看的图形如图1所示．

    这个几何体可以是图2中甲，乙，丙中的______；

    这个几何体最多由______个小正方体堆成，最少由______个小正方体堆成；

    请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于E交AB的延长线于点F．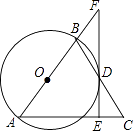

    （1）求证：EF是⊙O的切线；
    （2）若AE=6，FB=4，求⊙O的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

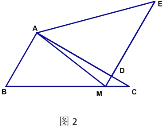
    【题目】将一副三角板拼成如图所示的图形，即，，，，与相交于点．

    　　　　　　　

    （1）如果，那么与平行吗？试说明理由；

    （2）将绕着点逆时针旋转，使得点落在边上，联结并延长交于点，联结，若，，，求的面积．

    查看答案和解析>>

    同步练习册答案