
 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
 ;(2)
;(2)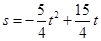 ,
,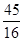 ;(3)当
;(3)当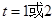 时,四边形BCMN为平行四边形;当
时,四边形BCMN为平行四边形;当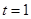 时,平行四边形BCMN为菱形
时,平行四边形BCMN为菱形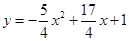 即可求得B点的坐标,再把点B的坐标代入
即可求得B点的坐标,再把点B的坐标代入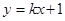 即可求得直线AB的函数关系式;
即可求得直线AB的函数关系式; 和
和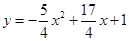 即可得到点M、N的纵坐标,从而可以表示出MN的长,再根据二次函数的性质求解即可;
即可得到点M、N的纵坐标,从而可以表示出MN的长,再根据二次函数的性质求解即可;
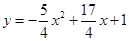 ,得
,得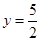 ,
,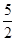 )
)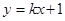 ,得
,得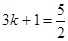 ,解得
,解得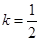
 ;
; 和
和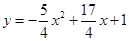
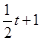 、
、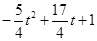
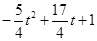 -(
-(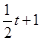 )=
)=

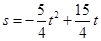 =-
=-
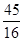 ;
;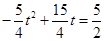 ,得
,得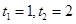
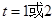 时,四边形BCMN为平行四边形
时,四边形BCMN为平行四边形 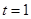 时,PC=2,PM=
时,PC=2,PM=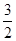 ,由勾股定理求得CM =
,由勾股定理求得CM =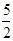
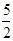 ,平行四边形BCMN为菱形;
,平行四边形BCMN为菱形;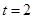 时,PC=1,PM=2,由勾股定理求得CM=
时,PC=1,PM=2,由勾股定理求得CM=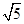
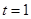 时,平行四边形BCMN为菱形.
时,平行四边形BCMN为菱形.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.0<t<2 | B.0<t<1 | C.1<t<2 | D.﹣1<t<1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
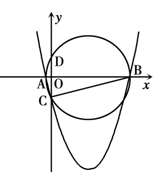
 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点 、
、 ,与
,与 轴的交点为
轴的交点为 .设
.设 的外接圆的圆心为点
的外接圆的圆心为点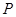 .
.
 与
与 轴的另一个交点D的坐标;
轴的另一个交点D的坐标; 恰好为
恰好为 的直径,且
的直径,且 的面积等于
的面积等于 ,求
,求 和
和 的值.
的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com