
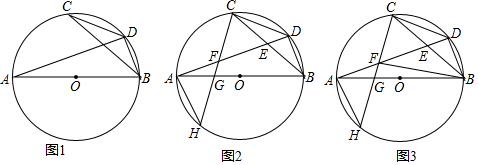
分析 (1)连接AC.由$\widehat{AC}$=$\widehat{BC}$,推出∠CBA=∠CAB=∠CAD+∠DAB,由$\widehat{CD}$=$\widehat{CD}$,$\widehat{BD}$=$\widehat{BD}$,推出∠DCB=∠DAB,∠CBD=∠CAD,推出∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA.
(2)只要证明△ACF△BCD,即可推出AF=BD.
(3)由△ACK≌△CNM,推出AK=CM,由△ACF≌△BCD,推出CF=CD,△AFK是等腰直角三角形,推出AK=FK=FM=CM,在Rt△AKC中,tan∠CAK=$\frac{CK}{AK}$=3,作EN⊥CH于N,在Rt△NCE中,由∠HCB=∠CAK,推出tan∠NCE=$\frac{EN}{CN}$=3,设CN=m,EN=3m=NF,由S△CEF=$\frac{1}{2}$•CF•EN=$\frac{1}{2}$×(m+3m)×3m,推出m=$\frac{\sqrt{2}}{2}$,推出CF=4m=2$\sqrt{2}$,推出CM=FM=FK=AK=$\sqrt{2}$,AF=2,由$\widehat{DB}$=$\widehat{DB}$,推出∠DCB=∠DAB=∠ACK,过G作GQ⊥AF于Q,在Rt△AQG中,tan∠FAB=$\frac{QG}{AQ}$=$\frac{1}{3}$,设QG=x,AQ=3x,FQ=x,可得4x=2,得x=$\frac{1}{2}$,再根据FG=$\sqrt{2}$QG即可解决问题.
解答 (1)证明:连接AC,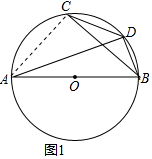
在⊙O中,∵C为$\widehat{AB}$的中点,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠CBA=∠CAB=∠CAD+∠DAB,
∵$\widehat{CD}$=$\widehat{CD}$,$\widehat{BD}$=$\widehat{BD}$,
∴∠DCB=∠DAB,∠CBD=∠CAD,
∴∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA.
(2)证明:连接AC.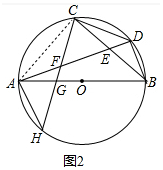
∵AB是直径,
∴∠ACB=90°=∠ACF+∠FCB,
∵CD⊥CH,
∴∠DCH=90°=∠FCB+∠DCB,
∴∠ACF=∠DCB,
∵$\widehat{AC}$=$\widehat{BC}$,
∴AC=BC,
在△ACF和△BCD中,
$\left\{\begin{array}{l}{∠ACF=∠DCB}\\{AC=BC}\\{∠CAF=∠CBD}\end{array}\right.$,
∴△ACF≌△BCD,
∴AF=BD.
(3)解:作BM⊥CH于M,AK⊥CH于K.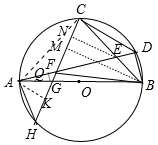
∴∠ACK+∠CAK=90°,∠AKC=∠BMC=90°,
∵∠ACB=90°,
∴∠ACK+∠KCB=90°,
∴∠CAK=∠KCB,∵AC=BC,
∴△ACK≌△CNM,
∴AK=CM,
∵CB=BF,BM⊥CF,
∴CM=FM=AK,
∵△ACF≌△BCD,
∴CF=CD,
∵∠FCD=90°,
∴∠CFD=∠CDF=45°=∠AFK,
∴△AFK是等腰直角三角形,
∴AK=FK=FM=CM,
在Rt△AKC中,tan∠CAK=$\frac{CK}{AK}$=3,作EN⊥CH于N,
在Rt△NCE中,∵∠HCB=∠CAK,
∴tan∠NCE=$\frac{EN}{CN}$=3,设CN=m,EN=3m=NF,
∴S△CEF=$\frac{1}{2}$•CF•EN=$\frac{1}{2}$×(m+3m)×3m=3,
∴m=$\frac{\sqrt{2}}{2}$,
∴CF=4m=2$\sqrt{2}$,
∴CM=FM=FK=AK=$\sqrt{2}$,
∴AF=2,
∵$\widehat{DB}$=$\widehat{DB}$,
∴∠DCB=∠DAB=∠ACK,
过G作GQ⊥AF于Q,
在Rt△AQG中,tan∠FAB=$\frac{QG}{AQ}$=$\frac{1}{3}$,设QG=x,AQ=3x,FQ=x,
∴4x=2,
∴x=$\frac{1}{2}$,
∴FG=$\sqrt{2}$x=$\frac{\sqrt{2}}{2}$.
点评 本题考查圆综合题、全等三角形的判定和性质、等腰直角三角形的性质和判定、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数,构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=0}\\{y+1=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=4}\\{y+z=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{xy=4}\\{3x+y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{{x}^{2}-y=4}\\{x+y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
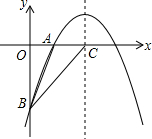 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过A(2,0)、B(0,-6)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com