
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

【答案】(1)证明见解析;(2)当∠BAE≠90°时,(1)的结论仍成立,理由见解析.
【解析】
(1)因为AF是直角三角形ABE的中线,所以BE=2AF,然后通过△ABE≌△ACD即可求得.
(2)延长EA交BC于G,在AG上截取AH=AD,证出△ABH≌△ACD从而证得BH=CD,然后根据三角形的中位线等于底边的一半,求得BH=2AF,即可求得.
(1)如图①.
∵∠BAC+∠EAD=180°,∠BAE=90°,∴∠DAC=90°.
在△ABE与△ACD中,
∵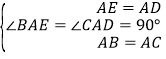 ,
,
∴△ABE≌△ACD(SAS),∴CD=BE.
∵在Rt△ABE中,F为BE的中点,∴BE=2AF,∴CD=2AF.
(2)成立.理由如下:
如图②,延长EA交BC于G,在AG上截取AH=AD.
∵∠BAC+∠EAD=180°,∴∠EAB+∠DAC=180°.
∵∠EAB+∠BAH=180°,∴∠DAC=∠BAH.
在△ABH与△ACD中,∵ ,
,
∴△ABH≌△ACD(SAS),
∴BH=DC.
∵AD=AE,AH=AD,∴AE=AH.
∵EF=FB,∴BH=2AF,∴CD=2AF.


科目:初中数学 来源: 题型:
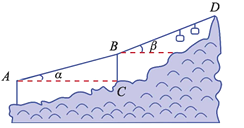
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ADC=90°,点E是BC边上一动点,联结AE,过点E作AE的垂线交直线CD于点F.已知AD=4cm,CD=2cm,BC=5cm,设BE的长为x cm,CF的长为y cm.

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:

(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题: 当BE=CF时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的横坐标为x,纵坐标为2x,满足这样条件的点称为“关系点”.
(1)在点A(1,2)、B(2,1)、M(![]() ,1)、N(1,
,1)、N(1, ![]() )中,是“关系点”的为 ;
)中,是“关系点”的为 ;
(2)⊙O的半径为1,若在⊙O上存在“关系点”P,求点P坐标;
(3)点C的坐标为(3,0),若在⊙C上有且只有一个“关系点”P,且“关系点”P的横坐标满足-2≤x≤2.请直接写出⊙C的半径r的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点![]() 、
、![]() 、
、![]() 都是格点.
都是格点.

(1)将![]() 向左平移6个单位长度得到
向左平移6个单位长度得到![]() ;
;
(2)将![]() 绕点
绕点![]() 按逆时针方向旋转180°得到
按逆时针方向旋转180°得到![]() ,请画出
,请画出![]() ;
;
(3)若点![]() 的坐标为(3,3);写出
的坐标为(3,3);写出![]() 与
与![]() 的对称中心的坐标_____.
的对称中心的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
(1)如图①,![]() 中,
中,![]() ,若
,若![]() ,点
,点![]() 是斜边
是斜边![]() 上一动点,求线段
上一动点,求线段![]() 的最小值.
的最小值.

在组内经过合作交流,得到了如下的解决方法:
根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:
当![]() 时,线段
时,线段![]() 取得最小值.请你根据小明的思路求出这个最小值.
取得最小值.请你根据小明的思路求出这个最小值.
(思维运用)
(2)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一动点,过
上一动点,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求线段
,求线段![]() 的最小值.
的最小值.

(问题拓展)
(3)如图,![]() ,
,![]() 线段
线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() 在一条直线上.
在一条直线上.![]() ,
,![]() 分别是对角线
分别是对角线![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 之间的距离的最小值为_____.(直接写出结果,不需要写过程)
之间的距离的最小值为_____.(直接写出结果,不需要写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是□ABCD的边BC延长线上一点,AE交CD于点F,FG∥AD交AB于点G.
(1)填空:图中与△CEF相似的三角形有__________;(写出图中与△CEF相似的所有三角形)
(2)从(1)中选出一个三角形,并证明它与△CEF相似.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com