
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
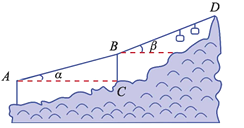
【答案】700sin20°+700sin16°+126
【解析】试题分析:本题考查了解直角三角形的实际应用,在Rt△ABC中,根据![]() 可求出BC的长度;在Rt△BDE中,根据
可求出BC的长度;在Rt△BDE中,根据![]() 可求出DE的长度;从而可求出D点的海拔高度.
可求出DE的长度;从而可求出D点的海拔高度.
解:如图,
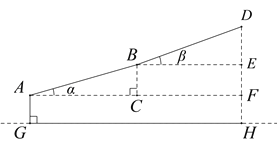
在Rt△ABC中,∠ACB=90°,∠![]() =16°,AB=700,由sin
=16°,AB=700,由sin![]() ,可求BC的长.
,可求BC的长.
即BC=AB·sin![]() =700sin16°,在Rt△BDE中,∠DBE=90°,∠β=16°,BD=AB=700,由sinβ,可求DE的长.
=700sin16°,在Rt△BDE中,∠DBE=90°,∠β=16°,BD=AB=700,由sinβ,可求DE的长.
即DE=BD·sinβ=700sin20°,由矩形性质,可知EF=BC=700sin16°,FH=AG=126.
从而,可求得DH的长.
即DH=DE+EF+FH=700sin20°+700sin16°+126.


科目:初中数学 来源: 题型:
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.
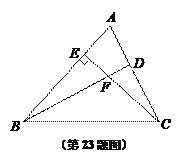
(1)求证:BD⊥AC;
(2)联结AF,求证:AF·BE=BC·EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°。
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图像,请根据图像所提供的信息,求该公路的总长度.
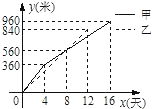
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,连接BE,CD,F为BE的中点,连接AF.
(1)如图①,当∠BAE=90°时,求证:CD=2AF;
(2)当∠BAE≠90°时,(1)的结论是否成立?请结合图②说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com