
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

【答案】壁虎捕捉蚊子的最短距离为1.3m.
【解析】
将容器侧面展开,建立A关于EC的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
解:如图:作A关于EC的对称点A′,连接A′B交EC于点F,则壁虎沿AF、FB捕捉蚊子距离最短.作A′D⊥BC交BC的延长线于D,则四边形A′DCE是矩形.
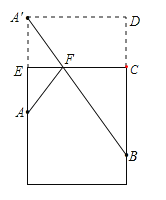
∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,壁虎离容器上沿0.3m处,
∴A′D=0.5m,A′E=AE=0.3m,BC=1.2-0.3=0.9m,
∴BD=BC+CD=0.9+0.3=1.2m,
∴A′B=![]() =
=![]() =1.3(m).
=1.3(m).
故壁虎捕捉蚊子的最短距离为1.3m.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
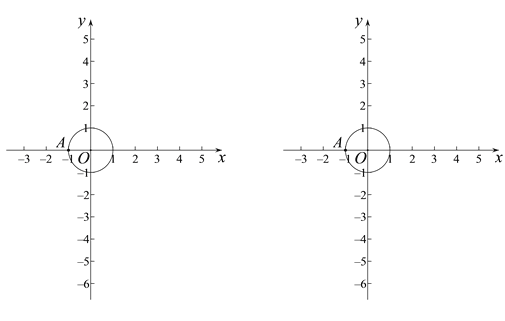
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明在玩纸片拼图游戏时,发现利用图①中的三种材料各若干,可以拼出一些长方形来解释某些等式,比如图②可以解释为等式:![]() .
.

(1)则图③可以解释为等式: .
(2)在虚线框中用图①中的基本图形若干块(每种至少用一次)拼成一个长方形,使拼出的长方形面积为![]() ,并请在图中标出这个长方形的长和宽.
,并请在图中标出这个长方形的长和宽.
(3)如图④,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,若用
,若用![]() 、
、![]() 表示四个长方形的两边长(
表示四个长方形的两边长(![]() ),观察图案,指出以下关系式:(
),观察图案,指出以下关系式:(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)![]() ; (
; (![]() )
)![]() .其中正确的关系式的个数有 个.
.其中正确的关系式的个数有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
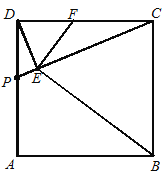
【题目】如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )

A.y=![]() x+5B.y=
x+5B.y=![]() x+5C.y=
x+5C.y=![]() x+5D.y=
x+5D.y=![]() x+5
x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
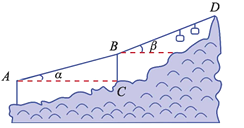
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com