练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图：在六边形ABCDEF中，AF∥CD，AB∥DE，∠BAF=100°，∠BCD=120°.

    求∠ABC和∠D的度数．

    【答案】∠CDE=100°；∠ABC=140°.

    【解析】

    连接AD，由AF∥CD得出∠FAD=∠ADC，由AB∥DE得出∠BAD=∠ADE，故可得出∠CDE=∠BAF=100°，∠FAD+∠BAD=∠ADC+∠BAD=100°，再由四边形内角和定理即可得出∠ABC的度数．

    解：连接AD

    ∵AF∥CD，AB∥DE，

    ∴∠FAD=∠ADC，∠BAD=∠ADE，

    ∴∠BAF=∠CDE=100°

    ∵∠ABC+∠DCB+∠BAD+∠ADC=360°，

    又∵∠FAB=∠FAD+∠BAD=∠ADC+∠BAD=100°，

    ∴∠ABC=360°-120°-100°=140°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图在平面直角坐标系xOy中，函数y1＝(x＞0)的图象与一次函数y2＝kx－k的图象的交点为A(m，2)．

    (1)求一次函数的解析式；

    (2)设一次函数y＝kx－k的图象与y轴交于点B，若点P是x轴上一点，且满足△PAB的面积是6，请写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某实验学校校友会在今年开学初，到新华书店采购文学名著和自然科学两类图书．经了解，购买30本文学名著和50本自然科学书共需2350元，20本文学名著比20本自然科学书贵500元．

    （1）求每本文学名著和自然科学书的单价．

    （2）若该校校友会要求购买自然科学书比文学名著多30本，总费用不超过2400元，请求出至多购买文学名著多少本？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，求壁虎捕捉蚊子的最短距离．（容器厚度忽略不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作翻转变换，依次得到△1、△2、△3、△4…，则△23中的的坐标为_______________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为培养学生的特长爱好，提髙学生的综合素质，某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同，每个竖笛的价格相同)，购买2个竖笛和1个尤克里里共需290元；竖笛单价比尤克里里单价的一半少25元．

    (1)求竖笛和尤克里里的单价各是多少元？

    (2)根据学校实际情况，需一次性购买竖笛和尤克里里共20个，但要求购买竖笛和尤克里里的总费用不超过3450元，则该校最多可以购买多少个尤克里里？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线y＝﹣x+m经过点A（2，0），交y轴于点B．点D为x轴上一点，且S△ADB＝1．

    （1）求m的值；

    （2）求线段OD的长；

    （3）当点E在直线AB上（点E与点B不重合），且∠BDO＝∠EDA，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，在锐角△ABC中，CE⊥AB于点E，点D在边AC上，联结BD交CE于点F，且EF·FC=FB·DF.

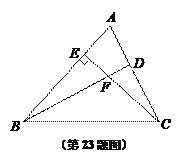
    （1）求证：BD⊥AC；

    （2）联结AF，求证：AF·BE=BC·EF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县在实施“村村通”工程中，决定在A、B两村之间修筑一条公路，甲、乙两个工程队分别从A、B两村同时相向开始修筑．施工期间，乙队因另有任务提前离开，余下的任务由甲队单独完成，直到道路修通．下图是甲、乙两个工程队所修道路的长度y（米）与修筑时间x（天）之间的函数图像，请根据图像所提供的信息，求该公路的总长度．

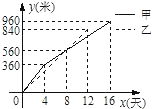
    查看答案和解析>>

    同步练习册答案