
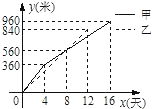
【题目】某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图像,请根据图像所提供的信息,求该公路的总长度.
科目:初中数学 来源: 题型:
【题目】顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,直接写出AB与DE的位置关系;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成和对称的格点三角形AFC,直接写出△BCF是什么形状的特殊三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
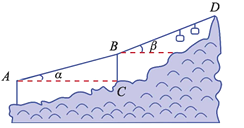
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
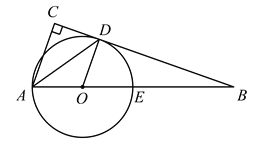
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)在第__________次记录时距![]() 地最远;
地最远;
(2)求收工时距![]() 地多远?
地多远?
(3)若每千米耗油![]() 升,每升汽油需
升,每升汽油需![]() 元,问检修小组工作一天需汽油费多少元?
元,问检修小组工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:
(1)如图①,![]() 中,
中,![]() ,若
,若![]() ,点
,点![]() 是斜边
是斜边![]() 上一动点,求线段
上一动点,求线段![]() 的最小值.
的最小值.

在组内经过合作交流,得到了如下的解决方法:
根据直线外一点和直线上各点连接的所有线段中,垂线段最短,得到:
当![]() 时,线段
时,线段![]() 取得最小值.请你根据小明的思路求出这个最小值.
取得最小值.请你根据小明的思路求出这个最小值.
(思维运用)
(2)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 上一动点,过
上一动点,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,求线段
,求线段![]() 的最小值.
的最小值.

(问题拓展)
(3)如图,![]() ,
,![]() 线段
线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() 在一条直线上.
在一条直线上.![]() ,
,![]() 分别是对角线
分别是对角线![]() 的中点,当点
的中点,当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() 之间的距离的最小值为_____.(直接写出结果,不需要写过程)
之间的距离的最小值为_____.(直接写出结果,不需要写过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com