
【题目】如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.
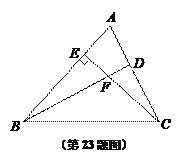
(1)求证:BD⊥AC;
(2)联结AF,求证:AF·BE=BC·EF.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由两边成比例且夹角相等的两个三角形相似,可得△EFB∽△DFC,再由相似三角形对应角相等得∠FEB=∠FDC = 90°,即可得证;
(2)由△EFB∽△DFC得∠ABD =∠ACE,进而△AEC∽△FEB,由相似三角形对应边成比例得![]() ,由此△AEF∽△CEB,可得
,由此△AEF∽△CEB,可得![]() .
.
试题解析:(1)∵AF·BE=BC·EF ,
∴![]() ,
,
∵ ∠EFB=∠DFC,
∴ △EFB∽△DFC.
∴ ∠FEB=∠FDC.
∵ CE⊥AB,
∴ ∠FEB= 90°.
∴ ∠FDC= 90°.
∴ BD⊥AC.
(2)∵ △EFB∽△DFC,
∴ ∠ABD =∠ACE.
∵ CE⊥AB,
∴ ∠FEB= ∠AEC= 90°.
∴ △AEC∽△FEB.
∴![]() ,
,
∴![]() .
.
∵ ∠AEC=∠FEB= 90°,
∴ △AEF∽△CEB.
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】对于⊙C与⊙C上的一点A,若平面内的点P满足:射线AP与⊙C交于点Q(点Q可以与点P重合),且![]() ,则点P称为点A关于⊙C的“生长点”.
,则点P称为点A关于⊙C的“生长点”.
已知点O为坐标原点,⊙O的半径为1,点A(-1,0).
(1)若点P是点A关于⊙O的“生长点”,且点P在x轴上,请写出一个符合条件的点P的坐标________;
(2)若点B是点A关于⊙O的“生长点”,且满足![]() ,求点B的纵坐标t的取值范围;
,求点B的纵坐标t的取值范围;
(3)直线![]() 与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
与x轴交于点M,与y轴交于点N,若线段MN上存在点A关于⊙O的“生长点”,直接写出b的取值范围是_____________________________.
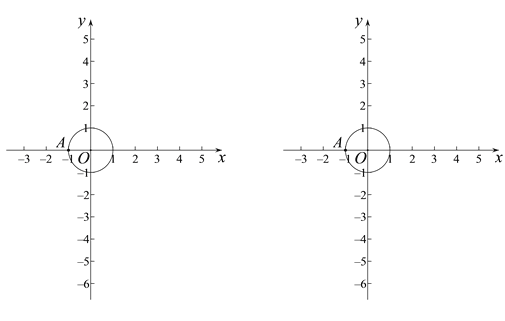
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为( )

A.y=![]() x+5B.y=
x+5B.y=![]() x+5C.y=
x+5C.y=![]() x+5D.y=
x+5D.y=![]() x+5
x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
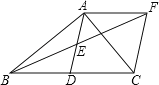
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在数轴上点A、B、C表示的数分别为﹣2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.

(1)则AB= ,BC= ,AC= ;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:BC﹣AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:随着运动时间t的变化,AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,直接写出AB与DE的位置关系;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成和对称的格点三角形AFC,直接写出△BCF是什么形状的特殊三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
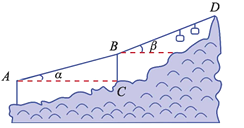
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com