
【题目】一天,小明在玩纸片拼图游戏时,发现利用图①中的三种材料各若干,可以拼出一些长方形来解释某些等式,比如图②可以解释为等式:![]() .
.

(1)则图③可以解释为等式: .
(2)在虚线框中用图①中的基本图形若干块(每种至少用一次)拼成一个长方形,使拼出的长方形面积为![]() ,并请在图中标出这个长方形的长和宽.
,并请在图中标出这个长方形的长和宽.
(3)如图④,大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]() ,若用
,若用![]() 、
、![]() 表示四个长方形的两边长(
表示四个长方形的两边长(![]() ),观察图案,指出以下关系式:(
),观察图案,指出以下关系式:(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)![]() ; (
; (![]() )
)![]() .其中正确的关系式的个数有 个.
.其中正确的关系式的个数有 个.
【答案】(1)(2a+b)(a+2b)=2a2+5ab+2b2;(2)画图略;(3)4.
【解析】
(1)看图即可得出所求的式子;
(2)画出的矩形边长分别为(2a+b)和(a+3b)即可;
(3)根据图中每个图形的面积之间的关系即可判断出正确的有几个.
解:(1)由分析知:图③所表示的等式为:(2a+b)(a+2b)=2a2+5ab+2b2;
(2)示意图如下
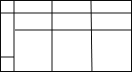 ;
;
(3)(a)观察图形可知正确;
(b)∵4xy=m2-n2,∴xy=![]() ,正确;
,正确;
(c)∵x+y=m,x-y=n,∴x2-y2=(x+y)(x-y)=mn,∴正确;
(d)x2+y2=(x-y)2+2xy=n2+2×![]() =
=![]() ,正确;
,正确;
故正确的有4个,故答案为:4.


科目:初中数学 来源: 题型:
【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字 1,2,3,5 的四张牌给小莉,将数字为 4,6,7,8 的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后 将抽出的两张牌数字相加,如果和为偶数,则小莉去,如果和为奇数,则哥哥去。
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平么?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.
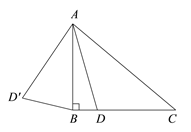
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,总费用不超过2400元,请求出至多购买文学名著多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作翻转变换,依次得到△1、△2、△3、△4…,则△23中的![]() 的坐标为_______________。
的坐标为_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com