
【题目】如图,正方形ABCD中,点P是AD上的一动点(与点D、点A不重合),DE⊥CP,垂足为E,EF⊥BE与DC交于点F.
(1)求证:△DEF∽△CEB;
(2)当点P运动到DA的中点时,求证:点F为DC的中点.
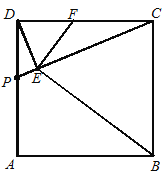
【答案】证明见解析
【解析】试题分析:(1)由DE⊥CP,EF⊥BE,则∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,根据等角的余角相等得∠1=∠2,再根据正方形的性质得∠4+∠6=90°,而∠4+∠5=90°,则∠5=∠6,根据相似三角形的判定即可得到结论;
(2)根据正方形的性质得AD=DC=BC,而点P为DA的中点,则PD=![]() AD=
AD=![]() DC,再根据正切的定义得到tan∠4=
DC,再根据正切的定义得到tan∠4=![]() ,tan∠4=
,tan∠4=![]() ,则
,则![]() ,然后根据△DEF∽△CEB得到
,然后根据△DEF∽△CEB得到![]() ,易得
,易得![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)∵DE⊥CP,EF⊥BE,
∴∠1+∠3=∠DEC=90°,∠2+∠3=∠FEB=90°,
∴∠1=∠2,
∵四边形ABCD是正方形,
∴∠4+∠6=∠DCB=90°,
而在Rt△DEC中,∠4+∠5=90°,
∴∠5=∠6,
∴△DEF∽△CEB;
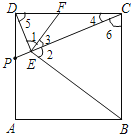
(2)∵四边形ABCD是正方形,
∴AD=DC=BC,
∵点P为DA的中点,
∴PD=![]() AD=
AD=![]() DC,
DC,
在Rt△PDC中,tan∠4=![]() ,
,
在Rt△DEC中,tan∠4=![]() ,
,
∴![]() ,
,
∵△DEF∽△CEB,
∴![]() ,
,
而CB=DC,
∴![]() ,
,
∴点F为DC的中点.


科目:初中数学 来源: 题型:
【题目】2019年3月25日是全国中小学生安全教育日,某中学为加强学生的安全意识,组织了全校800名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.


(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n=
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有大小、质地完全相同的2个白球和2个黑球.
(1) 先从袋中投出1个球后放回,混合均匀后再摸出1个球,则第一次摸到白球,第二次摸到黑球的概率为P1为__________;
(2) 若第一次从袋子中摸出1个球后不放回,第二次再摸出1个球,则两次摸到的球中有1个白球和1个黑球的概率P2是多少?(请用画树形图或列表法求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,![]() 表示数a在数轴上的对应点与原点的距离,如:5表示5在数轴上的对应点到原点的距离.而
表示数a在数轴上的对应点与原点的距离,如:5表示5在数轴上的对应点到原点的距离.而![]() ,即
,即![]() 表示5、0在数轴上对应的两点之间的距离,类似的,有:
表示5、0在数轴上对应的两点之间的距离,类似的,有:![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示5、-3在数轴上对应的两点之间的距离一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为
表示5、-3在数轴上对应的两点之间的距离一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为![]() .
.
请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和3的两点之间的距离是________;数轴上P、Q两点的距离为3,点P表示的数是2,则点Q表示的数是________.
(2)点A、B、C在数轴上分别表示有理数x、-3、1,那么A到B的距离与A到C的距离之和可表示为________(用含绝对值的式子表示);满足![]() 的x的值为________;
的x的值为________;
(3)试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,求壁虎捕捉蚊子的最短距离.(容器厚度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,高AD、BE相交于点O,AE=BE,BC=5,且BD=![]() CD.
CD.
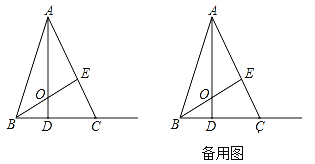
(1)①求证:△AOE≌△BCE;②求线段AO的长.
(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S,并直接写出t相应的的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生的特长爱好,提髙学生的综合素质,某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买2个竖笛和1个尤克里里共需290元;竖笛单价比尤克里里单价的一半少25元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共20个,但要求购买竖笛和尤克里里的总费用不超过3450元,则该校最多可以购买多少个尤克里里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
A. 120x=2×80(42-x) B. 80x=120(42-x)
C. 2×80x=120(42-x) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线EF分别与直线AB,CD相交于点O,M,射线OP在∠AOE的内部,且OP⊥EF,垂足为O,∠AOP=30°。
(1)若∠CME=120°,问AB和CD平行吗?为什么?
(2)若直线AB∥CD,求∠EMD的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com