
����Ŀ����ѧϰ����ֵ������֪����![]() ��ʾ��a�������ϵĶ�Ӧ����ԭ��ľ��룬�磺5��ʾ5�������ϵĶ�Ӧ�㵽ԭ��ľ���.��
��ʾ��a�������ϵĶ�Ӧ����ԭ��ľ��룬�磺5��ʾ5�������ϵĶ�Ӧ�㵽ԭ��ľ���.��![]() ����
����![]() ��ʾ5��0�������϶�Ӧ������֮��ľ��룬���Ƶģ��У�
��ʾ5��0�������϶�Ӧ������֮��ľ��룬���Ƶģ��У�![]() ��ʾ5��3�������϶�Ӧ������֮��ľ��룻
��ʾ5��3�������϶�Ӧ������֮��ľ��룻![]() ������
������![]() ��ʾ5��-3�������϶�Ӧ������֮��ľ���һ��أ���A��B�������Ϸֱ��ʾ������a��b����ôA��B֮��ľ���ɱ�ʾΪ
��ʾ5��-3�������϶�Ӧ������֮��ľ���һ��أ���A��B�������Ϸֱ��ʾ������a��b����ôA��B֮��ľ���ɱ�ʾΪ![]() .
.
����ݾ���ֵ�����岢����������������⣺
��1�������ϱ�ʾ2��3������֮��ľ�����________��������P��Q����ľ���Ϊ3����P��ʾ������2�����Q��ʾ������________.
��2����A��B��C�������Ϸֱ��ʾ������x��-3��1����ôA��B�ľ�����A��C�ľ���֮�Ϳɱ�ʾΪ________���ú�����ֵ��ʽ�ӱ�ʾ��������![]() ��x��ֵΪ________��
��x��ֵΪ________��
��3������![]() ����Сֵ.
����Сֵ.
���𰸡���1��1��5��-1����2��![]() ��-3��4����3��2500
��-3��4����3��2500
��������
��1�������������Ϸֱ��ʾ������a��b����ôA��B֮��ľ���ɱ�ʾΪ![]() �����뼴����⣻
�����뼴����⣻
��2����������������֮��ľ��빫ʽ�ɵ�A��B�ľ�����A��C�ľ��룻����![]() ��x��ֵ������������ۼ�����⣻
��x��ֵ������������ۼ�����⣻
��3����![]()
��Ϊ![]()
�ֱ����![]() ��
��![]() ��
��![]() ��50��x��51ʱȥ��Сֵ�������.
��50��x��51ʱȥ��Сֵ�������.
��1�������ϱ�ʾ2��3������֮��ľ�����3-2=1��
������P��Q����ľ���Ϊ3����P��ʾ������2�����Q��ʾ������2-3=-1��2+3=5��
��2��A��B�ľ�����A��C�ľ���֮�Ϳɱ�ʾΪ![]() ��
��
��![]()
��x��-2ʱ��3-x-x-2=7 �����x=-3
��-2��x��3��x������
��x��3ʱ��x-3+x+2=7,���x=4
������![]() ��x��ֵΪ-3��4;
��x��ֵΪ-3��4;
��3��![]() =
=![]()
��1��x��100��![]() ����СֵΪ
����СֵΪ![]() =99��
=99��
��2��x��99��![]() ����СֵΪ
����СֵΪ![]() =97��
=97��
...
��50��x��51��![]() ����СֵΪ
����СֵΪ![]() =1��
=1��
�൱50��x��51��![]() ����СֵΪ99+97+95+��+3+1=��99+1��+��97+3��+��95+5��+��+��51+49��=100��25=2500.
����СֵΪ99+97+95+��+3+1=��99+1��+��97+3��+��95+5��+��+��51+49��=100��25=2500.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪij���в��ֵֽ�ʾ��ͼ,�ı���ABCDΪ������,��G�ڶԽ���BD��,GE��CD,GF��BC,AD=1 500 m,С�����ߵ�·��ΪB��A��G��E,С�����ߵ�·��ΪB��A��D��E��F.��С�����ߵ�·��Ϊ3 100 m,��С�����ߵ�·��Ϊ �� m.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ij����������������Ŀģ�⿼��ʱ10��ͬѧ�IJ��Գɼ�����λ����/���ӣ�
�ɼ�����/���ӣ� | 140 | 160 | 169 | 170 | 177 | 180 |
���� | 1 | 1 | 1 | 2 | 3 | 2 |
�������10��ͬѧÿ���������IJ��Գɼ�������˵��������ǣ� ��
A.������135B.ƽ������170C.��λ����173.5D.������177
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C= 90����D��BC����һ�㣬��DBΪֱ���ġ�O����AB���е�E����AD���ӳ����ڵ�F������EF��
��1����֤����1= ��F��
��2����CD= 3��EF=![]() �����O�İ뾶����
�����O�İ뾶����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����ϵ�У�һ�κ���y=ax+b����κ���y=ax2��b��ͼ������ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߹���ͼ����д��������Ҫ������ͼ�ۼ���

��1����֪���߶�a�͡�������ͼ����������ABC��ʹ��AB=a����ABC=��������BAC=2������
��2���ڣ�1���������£�����ABC=360�����ACB�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
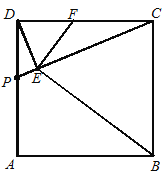
����Ŀ����ͼ��������ABCD�У���P��AD�ϵ�һ���㣨���D����A���غϣ���DE��CP������ΪE��EF��BE��DC���ڵ�F��
��1����֤����DEF�ס�CEB��
��2������P�˶���DA���е�ʱ����֤����FΪDC���е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݸ�������������һ�κ����ı���ʽ��
��1����֪һ�κ�����ͼ����ͼ��ʾ�����һ�κ����ı���ʽ�����жϵ㣨6��5���Ƿ��ڴ˺���ͼ���ϣ�
��2����ֱ֪��y��kx+bƽ����ֱ��y��3x+4���ҹ��㣨1��2�������ֱ�ߵĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ����������һ��ũ����Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊ20Ԫ/ǧ�ˣ��г����鷢�֣��ò�Ʒÿ���������w ��ǧ�ˣ������ۼ�x ��Ԫ/ǧ�ˣ������¹�ϵ��w=��2x+80�������ֲ�Ʒÿ�����������Ϊy ��Ԫ����
��1����y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3�������۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���28Ԫ/ǧ�ˣ���ũ����Ҫÿ����150Ԫ�������������ۼ�Ӧ��Ϊ����Ԫ�����ο���ϵ�����۶�=�ۼۡ�����������=���۶�ɱ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com