
����Ŀ����ͼ����ABC�У���AD��BE�ཻ�ڵ�O��AE��BE��BC��5����BD��![]() CD.
CD.
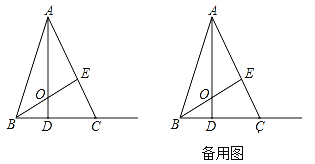
(1)����֤:��AOE�ա�BCE�������߶�AO�ij�.
(2)����P�ӵ�O���������߶�OA��ÿ��1����λ���ȵ��ٶ����յ�A�˶�������Q�ӵ�B����������BC��ÿ��4����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������P����A��ʱ��P��Q����ͬʱֹͣ�˶�.���P���˶�ʱ��Ϊt�룬��POQ�����ΪS�����ú�t��ʽ�ӱ�ʾS����ֱ��д��t��Ӧ�ĵ�ȡֵ��Χ.
���𰸡�(1)�ټ���������5����2��S��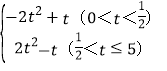
��������
(1) �ٸ���ASA֤����AOE�ա�BCE��
���ɢ�����AOE�ա�BCE�ɵ�AO��BC��5��
(2)����������������⼴�ɣ��ٵ���Q���߶�BD��ʱ��QD=2-4t���ڵ���Q������DC��ʱ��DQ=4t-2ʱ��
��1���١�AD�Ǹߣ�
���ADC=90����
��BE�Ǹߣ�
���AEB=��BEC=90����
���EAO+��ACD=90������EBC+��ECB=90����
���EAO=��EBC��
����AOE����BCE��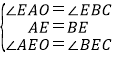 ��
��
���AOE�ա�BCE��
�ڡ���AOE�ա�BCE��
��AO=BC,
�֡�BC=5��
��AO��5;
��2����BD=![]() CD��BC=5��
CD��BC=5��
��BD=2��CD=3��
������OP=t��BQ=4t��
�ٵ���Q���߶�BD��ʱ��QD=2-4t��
��S=![]() t��2-4t��=-2t2+t��0��t��
t��2-4t��=-2t2+t��0��t��![]() ����
����
�ڵ���Q������DC��ʱ��DQ=4t-2��
��S=![]() t��4t-2��=2t2-t��
t��4t-2��=2t2-t��![]() ��t��5����
��t��5����
�ۺ������ɵã�S��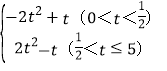 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��̽����
��1��һ�����������ͼ�ε�����ͼ������ͼ����ͼ1����ʾ��
���������������ǣ�ͼ2���ס����е��� ����
������������������� ����С�����幹�ɣ�����ͼ3�л���������������һ������ͼ��
��2����ͼ����֪һƽ���ڵ��ĸ���A��B��C��D������Ҫ����ֱ��ͼ��
�ٻ��߶�AB������AD��
����һ��M��ʹM�㼴������AD�ϣ�����ֱ��BC�ϣ�
����һ��N��ʹN��A��B��C��D�ĸ���ľ������̣�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C= 90����D��BC����һ�㣬��DBΪֱ���ġ�O����AB���е�E����AD���ӳ����ڵ�F������EF��
��1����֤����1= ��F��
��2����CD= 3��EF=![]() �����O�İ뾶����
�����O�İ뾶����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߹���ͼ����д��������Ҫ������ͼ�ۼ���

��1����֪���߶�a�͡�������ͼ����������ABC��ʹ��AB=a����ABC=��������BAC=2������
��2���ڣ�1���������£�����ABC=360�����ACB�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
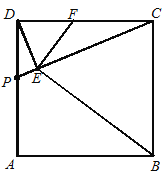
����Ŀ����ͼ��������ABCD�У���P��AD�ϵ�һ���㣨���D����A���غϣ���DE��CP������ΪE��EF��BE��DC���ڵ�F��
��1����֤����DEF�ס�CEB��
��2������P�˶���DA���е�ʱ����֤����FΪDC���е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪n���ε��ڽǺ�������n��2����180����
��1����ͬѧ˵������ȡ900��������ͬѧ˵����Ҳ��ȡ800�����ס��ҵ�˵���������ԣ��������n�������ԣ�˵�����ɣ�
��2����n���α�Ϊ��n+x�����Σ������ڽǺ�������540�������з��̵ķ���ȷ��x��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݸ�������������һ�κ����ı���ʽ��
��1����֪һ�κ�����ͼ����ͼ��ʾ�����һ�κ����ı���ʽ�����жϵ㣨6��5���Ƿ��ڴ˺���ͼ���ϣ�
��2����ֱ֪��y��kx+bƽ����ֱ��y��3x+4���ҹ��㣨1��2�������ֱ�ߵĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
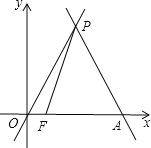
����Ŀ����֪����ͼ��ֱ��y����![]() x+4
x+4![]() ��x���ཻ�ڵ�A����ֱ��y��
��x���ཻ�ڵ�A����ֱ��y��![]() x���ڵ�P��
x���ڵ�P��
��1�����P�����꣮
��2������F��ԭ��O��������ÿ��1����λ���ٶ����߶�OA�����A�������˶�������PF�����˶�ʱ��Ϊt�룬��PFA�����ΪS�����S����t�ĺ�����ϵʽ��
��3������M��y��������һ�㣬��N������ƽ��������һ�㣬����O��M��N��PΪ������ı��������Σ���ֱ��д����N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
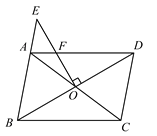
����Ŀ����ͼ������ABCD�����Խ���AC��BD���ڵ�O������O��EO��BD����BA�ӳ����ڵ�E����AD�ڵ�F����EF=OF����CBD=30����BD=![]() ����AF�ij���
����AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com