
 探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数an与层数n之间满足关系式an=n2-32n+247,n为正整数.例如,当n=1时,a1=12-32×1+247=216,
探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数an与层数n之间满足关系式an=n2-32n+247,n为正整数.例如,当n=1时,a1=12-32×1+247=216,

科目:初中数学 来源:2013学年浙江省杭州市拱墅区第一学期期末教学质量调研七年级数学试卷(带解析) 题型:填空题
探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数 与层数n之间满足关系式
与层数n之间满足关系式 ,
, 为正整数.
为正整数. 
例如,当 时,
时,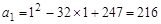 , 当
, 当 时,
时, ,则:
,则: = ,
= , = ;
= ;
⑵ 第n层比第(n+1)层多堆放 个货物箱.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源:2013学年浙江省杭州市拱墅区第一学期期末教学质量调研七年级数学试卷(解析版) 题型:填空题
探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数 与层数n之间满足关系式
与层数n之间满足关系式 ,
, 为正整数.
为正整数.

例如,当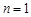 时,
时, , 当
, 当 时,
时, ,则:
,则:
 = ,
= , = ;
= ;
⑵ 第n层比第(n+1)层多堆放 个货物箱.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数an与层数n之间满足关系式
探索规律:货物箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放货物箱的个数an与层数n之间满足关系式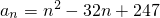 ,n为正整数.例如,当n=1时,
,n为正整数.例如,当n=1时,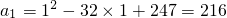 ,
,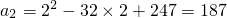 ,则:
,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com