
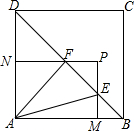
 如图,正方形ABCD的边长为2,P是△BCD内一动点,过点P作PM⊥AB于M,PN⊥AD于N,分别于对角线BD相交于点E,F.记PM=a,PN=b,当点P运动时,ab=2.
如图,正方形ABCD的边长为2,P是△BCD内一动点,过点P作PM⊥AB于M,PN⊥AD于N,分别于对角线BD相交于点E,F.记PM=a,PN=b,当点P运动时,ab=2.| 2 |
| 2 |
| DE |
| AB |
| AD |
| BF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| 2 |
| a |
| b |
| DE |
| AM |
| BD |
| AB |
| 2 |
| BF |
| AN |
| BD |
| AD |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| DE |
| AB |
| AD |
| BF |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| b |
| ab |
| ab |
| a |
| b |
| ab |
| a |
| b |
| 2 |
| a |
| b |
| a |
| b |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.
已知:如图,在△ABC中,点D是BC中点,点E是AC中点,且AD⊥BC,BE⊥AC,BE,AD相交于点G,过点B作BF∥AC交AD的延长线于点F,DF=6.| S△AEG |
| S△FBG |
查看答案和解析>>
科目:初中数学 来源: 题型:
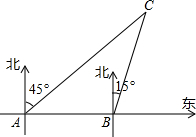 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
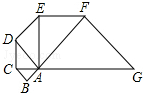 如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2014个等腰直角三角形的斜边长是
如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2014个等腰直角三角形的斜边长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com