
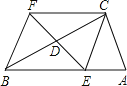
【题目】如图,在△ABC中,∠ACB=90°,且DE是△ABC的中位线.延长ED到F,使DF=ED,连接FC,FB.回答下列问题:
(1)试说明四边形BECF是菱形.
(2)当![]() 的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,菱形BECF是正方形?请回答并证明你的结论.
【答案】(1)见解析;(2)当∠A=45°时,菱形BECF是正方形.
【解析】(1)根据已知条件发现:可以证明四边形的对角线互相垂直平分即是一个菱形.
(2)菱形要是一个正方形,则根据正方形的对角线平分一组对角,即∠BEF=45°,则∠A=45°.
详(1)证明:∵DE是△ABC的中位线,
∴DE∥AC.
又∵∠ACB=90°,
∴EF⊥BC.
又∵BD=CD,DF=ED,
∴四边形BECF是菱形.
(2)解:要使菱形BECF是正方形
则有BE⊥CE
∵E是△ABC的边AB的中点
∴当△CBA是等腰三角形时,满足条件
∵∠BCA=90°
∴△CBA是等腰直角三角形
∴当∠A=45°时,菱形BECF是正方形.


科目:初中数学 来源: 题型:
【题目】三五三七鞋厂为了了解初中学生穿鞋的鞋号情况,对红华中学初二(1)班的20名男生所穿鞋号统计如下表:
鞋号 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
人数 | 3 | 4 | 4 | 7 | 1 | 1 |
(1)写出男生鞋号数据的平均数,中位数,众数;
(2)在平均数,中位数和众数中,鞋厂最感兴趣的是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.



(1)画一个底边为4,面积为8的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个面积为12的平行四边形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+6x+c(a≠0)交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,﹣5),点B的坐标为(1,0).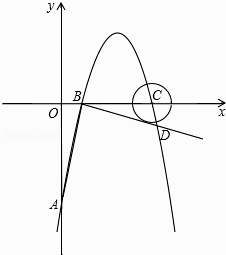
(1)求此抛物线的解析式及定点坐标;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并说明理由;
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD. 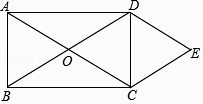
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为10 ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中学生对待学习的态度一直是教育工作者极为关注的一个问题.为此市教育局对本市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:喜欢;B级:不太喜欢;C级:不喜欢),并将调查结果绘制成图1和图2的统计图(不完整).请根据图中提供的信息,解答下列问题: 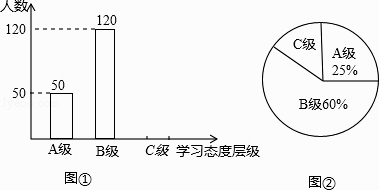
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该市近80000名初中生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
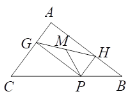
A. 2.4 B. 1.4
C. 1.3 D. 1.2
【答案】D
【解析】分析: 由AC=3、AB=4、BC=5,得AC2+AB2=BC2,则∠A=90°,再结合PG⊥AC,PH⊥AB,可证四边形AGPH是矩形;连接AP,可知当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法,求出GH的值,
详解:∵AC=3、AB=4、BC=5,
∴AC2=9,AB2=16,BC2=25,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90° ,
∴四边形AGPH是矩形.
连接AP,
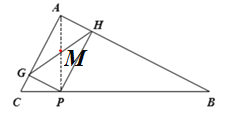
∴GH=AP.
∵当AP⊥BC时,AP最短,
∴3×4=5AP,
∴AP=![]() ,
,
∴PM的最小值为1.2.
故选D.
点睛: 本题考查了勾股定理的逆定理,矩形的判定与性质,垂线段最短,面积法求线段的长,需结合矩形的判定方法,矩形的性质以及三角形面积的知识求解;确定出点P的位置是解答本题的关键.
【题型】单选题
【结束】
18
【题目】计算:
(1)![]() (2)
(2)![]()
(3)![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com