
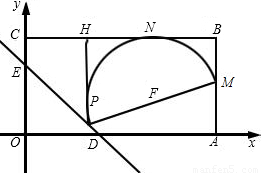
 (2007•韶关)如图,在平面直角坐标系中,四边形OABC是矩形,OA=4,AB=2,直线
(2007•韶关)如图,在平面直角坐标系中,四边形OABC是矩形,OA=4,AB=2,直线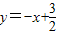 与坐标轴交于D、E.设M是AB的中点,P是线段DE上的动点.
与坐标轴交于D、E.设M是AB的中点,P是线段DE上的动点.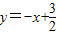 与坐标轴交于D、E,M是AB的中点,所以令y=0,即可求出D的坐标,而AM=1,所以M(4,1);
与坐标轴交于D、E,M是AB的中点,所以令y=0,即可求出D的坐标,而AM=1,所以M(4,1); 上,所以P(x,-x+
上,所以P(x,-x+ ,根据题意可得PN⊥MN,FN⊥BC,F是圆心,又因N是线段HB的中点,HN=NB=
,根据题意可得PN⊥MN,FN⊥BC,F是圆心,又因N是线段HB的中点,HN=NB=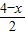 ,PH=2-(-x+
,PH=2-(-x+ )=x+
)=x+ ,BM=1,利用直径对的圆周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°,所以∠HPN=∠BNM,又因∠PHN=∠B=90°,所以可得到Rt△PNH∽Rt△NMB,所以
,BM=1,利用直径对的圆周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°,所以∠HPN=∠BNM,又因∠PHN=∠B=90°,所以可得到Rt△PNH∽Rt△NMB,所以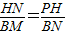 ,∴
,∴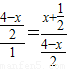 ,这样就可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以
,这样就可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以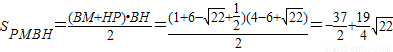 .
. ,0);(2分)
,0);(2分) 上,
上,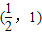 ;(4分)
;(4分)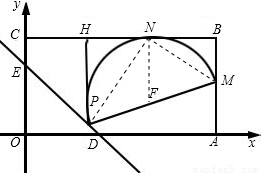 (3)设P(x,y),连接PN、MN、NF,
(3)设P(x,y),连接PN、MN、NF, 上,
上,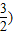 ,
,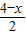 ,PH=2-(-x+
,PH=2-(-x+ )=x+
)=x+ ,BM=1,(6分)
,BM=1,(6分)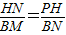 ,
,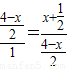 ,
,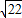
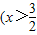 舍去),x=6-
舍去),x=6-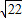 ,(8分)
,(8分)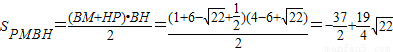 . (9分)
. (9分)

 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源:2007年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
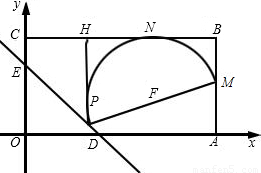 (2007•韶关)如图,在平面直角坐标系中,四边形OABC是矩形,OA=4,AB=2,直线
(2007•韶关)如图,在平面直角坐标系中,四边形OABC是矩形,OA=4,AB=2,直线 与坐标轴交于D、E.设M是AB的中点,P是线段DE上的动点.
与坐标轴交于D、E.设M是AB的中点,P是线段DE上的动点.查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《锐角三角函数》(05)(解析版) 题型:解答题
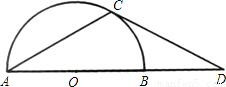
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《四边形》(10)(解析版) 题型:解答题
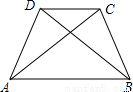
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com