
【题目】阅读下列两段材料,回答问题:
材料一:点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() .例如,点
.例如,点![]() ,
,![]() 的中点坐标为
的中点坐标为![]() ,即
,即![]()
材料二:如图1,正比例函数![]() 和
和![]() 的图象相互垂直,分别在
的图象相互垂直,分别在![]() 和
和![]() 上取点
上取点![]() 、
、![]() 使得
使得![]() 分别过点
分别过点![]() 作
作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() .显然,
.显然,![]() ,设
,设![]() ,
,![]() ,则
,则![]() ,
,![]() ..于是
..于是![]() ,
,![]() 所以
所以![]() 的值为一个常数,一般地,一次函数
的值为一个常数,一般地,一次函数![]() ,
,![]() 可分别由正比例函数
可分别由正比例函数![]() 平移得到.
平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数![]() ,
,![]() 的图象相互垂直,则
的图象相互垂直,则![]() 的值为一个常数.
的值为一个常数.
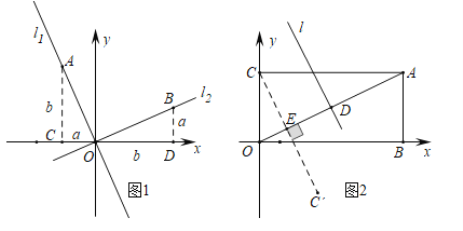
(1)在材料二中,![]() =______(写出这个常数具体的值)
=______(写出这个常数具体的值)
(2)如图2,在矩形![]() 中
中![]() ,点
,点![]() 是
是![]() 中点,用两段材料的结论,求点
中点,用两段材料的结论,求点![]() 的坐标和
的坐标和![]() 的垂直平分线
的垂直平分线![]() 的解析式;
的解析式;
(3)若点![]() 与点
与点![]() 关于
关于![]() 对称,用两段材料的结论,求点
对称,用两段材料的结论,求点![]() 的坐标.
的坐标.
【答案】(1)-1;(2) ![]() ,
, ![]() ;(3)
;(3)![]()
【解析】
(1)将k1,k2的值相乘,即可得出结论;
(2)由点O,A的坐标可求出其中点D的坐标,由点A的坐标可得出直线OA的解析式,由(1)的结论可设直线l的解析式为y=-2x+m,代入点D的坐标即可求出直线l的解析式;
(3)由矩形的性质可得出点C的坐标,由(1)的结论可设直线CC′的解析式为y=-2x+n,代入点C的坐标可求出直线CC′的解析式,联立直线CC′和OA的解析式成方程组,通过解方程组可求出点E的坐标,再由点E为线段CC′的中点可求出点C′的坐标.
(1)∵![]() =-
=-![]() ,
,![]() =
=![]() ,
,
∴k1k2=-![]()
![]() =-1.
=-1.
故答案为-1.
(2)∵点O的坐标为(0,0),点A的坐标为(4,2),点D是OA中点,
∴点D的坐标为(2,1).
∵点A的坐标为(4,2),
∴直线OA的解析式为y=![]() x.
x.
∵直线l⊥直线OA,
∴设直线l的解析式为y=-2x+m.
∵直线l过点D(2,1),
∴1=-4+m,解得:m=5,
∴OA的垂直平分线![]() 的解析式为y=-2x+5.
的解析式为y=-2x+5.
(3)∵点A的坐标为(4,2),四边形OBAC为矩形,
∴点C的坐标为(0,2).
设直线CC′的解析式为y=-2x+n,
∵直线CC′过点C(0,2),
∴n=2,即直线CC′的解析式为y=-2x+2.
联立直线CC′和OA的解析式成方程组,得: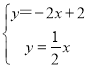 ,
,
解得:![]()
∴点E的坐标为(![]()
![]() )
)
∵点E为线段CC′的中点,
∴点C′的坐标为(![]()
![]() ),即(
),即(![]() -
-![]() ).
).
故答案为(1)-1;(2) ![]() ,
, ![]() ;(3)
;(3)![]()


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.
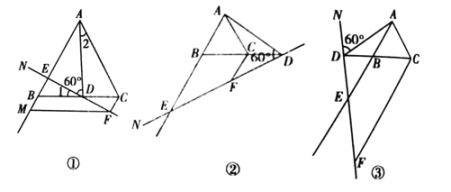
(1)当点D在线段BC上,∠NDB为锐角时,如图①.
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)①当点D在线段BC的延长线上,∠NDB为锐角时,如图②,请直接写出线段CF,BE,CD之间的数量关系;
②当点D在线段CB的延长线上,∠NDB为钝角或直角时,如图③,请直接写出线段CF,BE,CD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
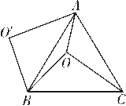
【题目】如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;&
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AOBO′的面积为6+3![]() ;
;
⑤S△AOC+S△AOB=6+![]() .
.
其中正确的结论是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
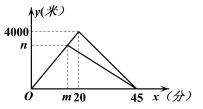
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x-3与坐标轴交于A、B两点,抛物线![]() 经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.
(1)求抛物线的解析式;
(2)抛物线上有一点M,当∠MBE=75°时,求点M的横坐标;
(3)点P在抛物线上,在坐标平面内是否存在点Q,使得以点P,Q,B,C为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
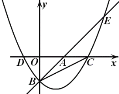

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于C,OC平分∠AOB.
(1)求∠AOB的度数;
(2)若线段CD的长为2cm,求![]() 的长度.
的长度.
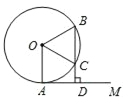
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
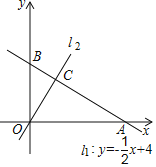
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com