
如图,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=![]() cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12 cm,动点P从点O开始沿OA以![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4 cm/s的速度向点B移动,动点R从点B开始沿BO以2 cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
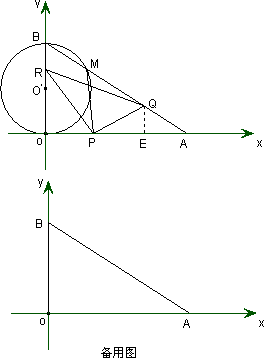
(1)求∠OAB的度数.
(2)以OB为直径的⊙![]() 与AB交于点M,当t为何值时,PM与⊙
与AB交于点M,当t为何值时,PM与⊙![]() 相切?
相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求s的最小值及相应的t值.
(4)是否存在△APQ为等腰三角形,若存在,求出相应的t值,若不存在请说明理由.
|
解:(1)在Rt△AOB中: tan∠OAB= ∴∠OAB=30° (2)如图,连接 △PM 由(1)知∠OBA=60° ∵ ∴△ ∴∠B 可得∠O ∴OP=O =6×tan60°= 又∵OP= ∴ 即:t=3时,PM与⊙
(3)如图,过点Q作QE⊥x于点E ∵∠BAO=30°,AQ=4t ∴QE= AE=AQ·cos∠OAB=4t× ∴OE=OA-AE= ∴Q点的坐标为( S△PQR=S△OAB-S△OPR-S△APQ-S△BRQ = = = 当t=3时,S△PQR最小= (4)分三种情况:如图. ①当AP=AQ1=4t时, ∵OP+AP= ∴ ∴t= 或化简为t=
②当PQ2=AQ2=4t时 过Q2点作Q2D⊥x轴于点D, ∴PA=2AD=2AQ2·cosA= 即 ∴t=2 ③当PA=PQ3时,过点P作PH⊥AB于点H AH=PA·cos30°=( AQ3=2AH=36-6t 得36-6t=4t, ∴t=3.6 综上所述,当t=2,t=3.6,t= |


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 8 |
| 14 |
| 3 |
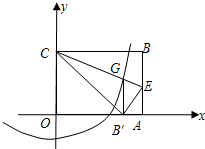 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.查看答案和解析>>
科目:初中数学 来源: 题型:
| a+2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com