
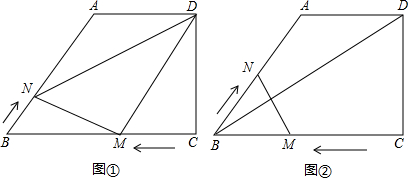
分析 (1)作AE⊥BC于E,根据直角梯形的性质和勾股定理求出AB的长;
(2)根据MN∥CD,则NM⊥BC,运用∠B的余弦求出时间t;
(3)根据△DMN的面积S=梯形ABCD的面积-△CDM的面积-△BMN的面积-△ADN的面积,代入数据整理即可;
(4)假设存在,经过推理求出时间t.
解答 解:(1)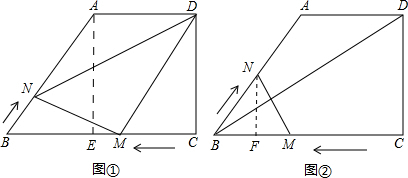 作AE⊥BC于E,
作AE⊥BC于E,
根据题意得,AE=DC=8,EC=AD=6,BE=BC-EC=6,
在Rt△ABE中,由勾股定理,AB=10.
(2)若MN∥CD,则NM⊥BC,
$\frac{BM}{BN}$=cosB=$\frac{6}{10}$=$\frac{3}{5}$,
即$\frac{12-2t}{t}$=$\frac{3}{5}$
解得:t=$\frac{60}{13}$秒.
(3)△DMN的面积S=梯形ABCD的面积-△CDM的面积-△BMN的面积-△ADN的面积
=$\frac{1}{2}$×(6+12)×8-$\frac{1}{2}$×2t×8-$\frac{1}{2}$×(12-2t)×$\frac{4}{5}$t-$\frac{1}{2}$×6×(8-$\frac{4}{5}$t)
=$\frac{4}{5}$(t-$\frac{13}{2}$)2+$\frac{71}{5}$,
又M从C点运动到B点的时间为6秒,N点从B点运动到A点所需的时间为10秒
依题意,两者取小值6秒,
所以,S=$\frac{4}{5}$(t-$\frac{13}{2}$)2+$\frac{71}{5}$ (0≤t≤6秒).
(4)假设存在,则有MN⊥BD,
显然有∠BMN=∠BDC,tan∠BMN=tan∠BDC=$\frac{BC}{CD}$=$\frac{12}{8}$=$\frac{3}{2}$,
如图②,过点N作NF⊥BC于F,
依题意可求得NF=$\frac{4}{5}$t,MF=12-2t-$\frac{3}{5}$t
所以,$\frac{NF}{MF}$=$\frac{\frac{4}{5}t}{12-2t-\frac{3}{5}t}$=tan∠BMN=$\frac{3}{2}$,
解得:t=$\frac{180}{47}$<6秒,符合题意.
所以存在t=$\frac{180}{47}$,使MN⊥BD.
点评 本题是四边形综合题,解答时用到锐角三角函数、二次函数、勾股定理、梯形的有关知识,综合性较强,需要学生熟练运用所学的知识,认真解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
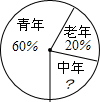 2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.
2015年1月份,某区体委组织“迎新春长跑活动”,现将报名的男选手分成:青年组、中年组、老年组,各组人数所占比例如图所示,已知青年组120人,则中年组的人数是40.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
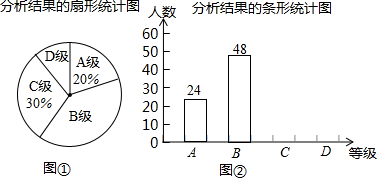
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 56 | B. | 560 | C. | 5600 | D. | 56000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
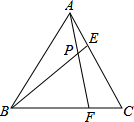 如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:
如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com