
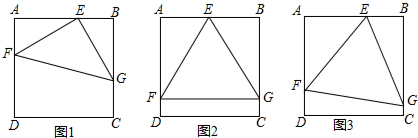
分析 (1)由△EFG是直角三角形,得到∠FEG=90°,于是得到∠AEF+∠BEG=90°,由于∠BEG+∠BGE=90°,得出∠AEF=∠BGE,在正方形ABCD中,∠A=∠B=90°,于是得到结论;
(2)由△EFG是等边三角形,点E是AB的中点,∠A=∠B=90°,得到Rt△AEF≌Rt△BEG,求出∠AEF=∠BEG=60°,∠BGE=30°,得到EG=2BE=AB,即可得到结论;
(3)如图3,作EK⊥FG于K,则K是FG的中点,连接AK,BK,得到∠EKG=∠EBG=∠EKF=∠EAF=90°,于是得出E、K、G、B和E、K、F、A分别四点共圆,推出△ABK是等边三角形,作KM⊥AB,则M为AB的中点,EB=$\frac{1}{3}$a,MB=$\frac{1}{2}$a,求出EM=$\frac{1}{6}$a,MK=asin60°=$\frac{\sqrt{3}}{2}$a,根据勾股定理得到EK=$\sqrt{{ME}^{2}{+MK}^{2}}$=$\frac{\sqrt{7}}{3}$a,推出EG=$\frac{EK}{sin60°}$=$\frac{2\sqrt{21}}{9}a$,求出BG=$\sqrt{{EG}^{2}{-BE}^{2}}$=$\frac{5\sqrt{3}}{9}a$,问题可得.
解答 (1)证明:∵△EFG是直角三角形,
∴∠FEG=90°,
∴∠AEF+∠BEG=90°,
∵∠BEG+∠BGE=90°,
∴∠AEF=∠BGE,
∵在正方形ABCD中,∠A=∠B=90°,
∴△AEF∽△BGE;
(2)解:∵△EFG是等边三角形,
∴EF=EG=FG,
∵点E是AB的中点,∠A=∠B=90°,
在Rt△AEF与Rt△BEG中,
$\left\{\begin{array}{l}{EF=EG}\\{AE=BE}\end{array}\right.$,
∴Rt△AEF≌Rt△BEG,
∴∠AEF=∠BEG=60°,
∴∠BGE=30°,
∴EG=2BE=AB,
∴BG=$\frac{\sqrt{3}}{2}$EG=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$BC,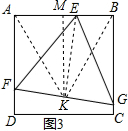
∴$\frac{BG}{BC}=\frac{\sqrt{3}}{2}$;
(3)解:如图3,作EK⊥FG于K,则K是FG的中点,连接AK,BK,
∴∠EKG=∠EBG=∠EKF=∠EAF=90°,
∴E、K、G、B和E、K、F、A分别四点共圆,
∴∠KBE=∠EGK=60°,∠EAK=∠EFK=60°,
∴△ABK是等边三角形,
作KM⊥AB,则M为AB的中点,EB=$\frac{1}{3}$a,MB=$\frac{1}{2}$a,
∴EM=$\frac{1}{6}$a,MK=asin60°=$\frac{\sqrt{3}}{2}$a,
∴EK=$\sqrt{{ME}^{2}{+MK}^{2}}$=$\frac{\sqrt{7}}{3}$a,
∴EG=$\frac{EK}{sin60°}$=$\frac{2\sqrt{21}}{9}a$,
∴BG=$\sqrt{{EG}^{2}{-BE}^{2}}$=$\frac{5\sqrt{3}}{9}a$,
∴$\frac{BG}{BC}=\frac{5\sqrt{3}}{9}$.
点评 本题考查了直角三角形的性质,正方形的性质,相似三角形的判定和性质,全等三角形的判定和性质,等边三角形的判定和性质,四点共圆,勾股定理,正确的作出辅助线是解题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
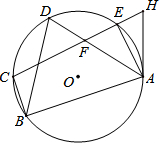 如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.
如图,点A、B、C、D、E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=$\sqrt{10}$,CH=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A发生的频率是$\frac{7}{100}$ | |
| B. | 反复大量做这种试验,事件A只发生了7次 | |
| C. | 做100次这种试验,事件A一定发生7次 | |
| D. | 做100次这种试验,事件A可能发生7次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com