
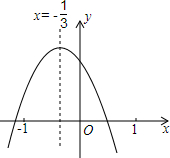 乐乐从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下列4条信息:
乐乐从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下列4条信息:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用x=1时,y<0可对①进行判断;利用抛物线的对称轴方程得到a=$\frac{3}{2}$b,则可对④进行判断;由于x=-1时,a-b+c>0,然后把a=$\frac{3}{2}$代入可对②进行判断;利用x=-$\frac{1}{2}$时,y>0可对④进行判断.
解答 解:∵x=1时,y<0,
即a+b+c<0,所以①正确;
∵抛物线的对称轴为直线x=-$\frac{b}{2a}$=-$\frac{1}{3}$,
∴a=$\frac{3}{2}$b,所以④正确;
∵x=-1时,y>0,
∴a-b+c>0,
∴$\frac{3}{2}$b-b+c>0,
即b+2c>0,所以②正确;
∵x=-$\frac{1}{2}$时,y>0,
∴$\frac{1}{4}$a-$\frac{1}{2}$b+c>0,
即a-2b+4c>0,所以③正确.
故选D.
点评 本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
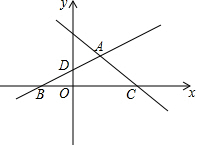 如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B.
如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与y轴交于点E.与直线AD交于点A($\frac{4}{3}$,$\frac{5}{3}$),点D的坐标为(0,1).直线AD与x轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知矩形ABCD的长AB=2,AB边与x轴重合,双曲线y=$\frac{k}{x}$在第一象限内经过D点以及BC的中点E.
已知矩形ABCD的长AB=2,AB边与x轴重合,双曲线y=$\frac{k}{x}$在第一象限内经过D点以及BC的中点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
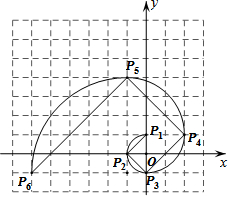 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$,$\widehat{{P_2}{P_3}}$,$\widehat{{P_3}{P_4}}$,…得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,…得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )| A. | (-6,24) | B. | (-6,25) | C. | (-5,24) | D. | (-5,25) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
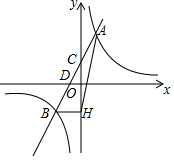 一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
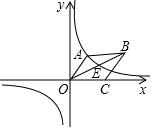 如图所示,已知四边形OABC是菱形,OC在x轴上,B(18,6),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A,与OB交于点E.
如图所示,已知四边形OABC是菱形,OC在x轴上,B(18,6),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点A,与OB交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的平行四边形是菱形 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 同位角相等 | |
| D. | 直角三角形斜边上的中线等于斜边的一半 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
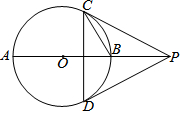 如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )
如图,AB是⊙O的直径,弦CD⊥AB,过点C作⊙O的切线与AB的延长线交于点P.若∠BCD=32°,则∠CPD的度数是( )| A. | 64° | B. | 62° | C. | 58° | D. | 52° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com