
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.

【答案】(1)作图见解析;(2)△CDB的周长为13.
【解析】
(1)根据垂直平分线的性质可得:线段垂直平分线的点到线段两端点距离相等, 作点D到点A的距离与点D到点C的距离相等,即作线段AC的垂直平分线与AB的交点即为点D.
(2)根据(1)可得DE垂直平分线线段AC,继而可得AD=DC,因此△CDB的周长=BC+BD+CD=BC+BD+AD=BC+AB,根据AB+AC+BC=21,BC=5,可得AB=AC=8,
因此△CDB的周长为13.
解:(1)点D如图所示,
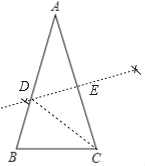
(2)∵DE垂直平分线线段AC,
∴AD=DC,
∴△CDB的周长=BC+BD+CD=BC+BD+AD=BC+AB,
∵AB+AC+BC=21,BC=5,
∴AB=AC=8,
∴△CDB的周长为13.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年5月新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.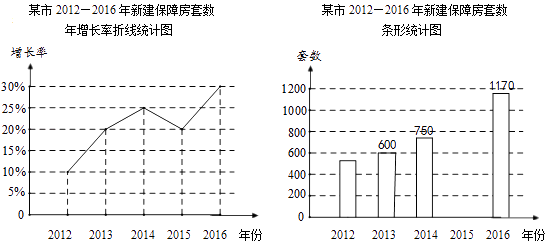
(1)小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() PAB的平分线与
PAB的平分线与![]() CBA的平分线相交于E,CE的延长线交AP于D,求证:
CBA的平分线相交于E,CE的延长线交AP于D,求证:
(1)AB=AD+BC;
(2)若BE=3,AE=4,求四边形ABCD的面积.
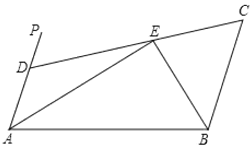
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s(km)与时间t(分钟)的函数关系图,观察图中所提供的信息,解答下列问题: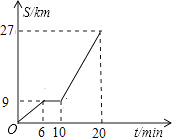
(1)汽车在前6分钟内的平均速度是千米/小时,汽车在兴国服务区停了多长时间?分钟;
(2)当10≤t≤20时,求S与t的函数关系式;
(3)规定:高速公路时速超过120千米/小时为超速行驶,试判断当10≤t≤20时,该汽车是否超速,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,请直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() =___.
=___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到![]() .
.

(1)画出平移后的![]() ;
;
(2)写出![]() 三个顶点的坐标;
三个顶点的坐标;
(3)已知点P在x轴上,以![]() 、
、![]() 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场推出A、B、C三种特价玩具,若购买A种2件、B种1件、C种3件,共需24元;若购买A种3件、B种4件、C种2件,共需36元.那么小明购买A种1件、B种1件、C种1件,共需付款( )
A.11元B.12元C.13元D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com