
���� ��1������һ������ˮ10�����ڣ�����10�֣����û���ÿ����1.5Ԫ��һ������ˮ����10�ֵ��û���10��ˮ��ÿ��1.5Ԫ�շѣ�����10�ֵIJ��֣���ÿ��2Ԫ�շѺ���ˮ������ÿ��0.65Ԫ����ʽ���㼴�ɣ�
��2��������������ۣ���0��x��10ʱ��x��10ʱ���ֱ������֪������ʽ�������ɣ�
��� �⣺��1����ˮ8��ʱ��Ӧ��ˮ���ǣ�1.5��8+0.65��8=17.2��Ԫ����
��ˮ16��ʱ��Ӧ��ˮ���ǣ�1.5��10+6��2+0.65��16=37.4��Ԫ����
��2���� 0��x��10ʱ��Ӧ����ˮ���ǣ�1.5x+0.65x=2.15xԪ��
��x��10ʱ��Ӧ����ˮ���ǣ�15+2��x-10��+0.65x=��2.65x-5��Ԫ��
���� ���⿼�����д���ʽ���������Ĺؼ��Ƕ������⣬�ҵ���������ĵ�����ϵ����ϵΪ��Ӧ��ˮ��=����ˮ��+��ˮ�����ѣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
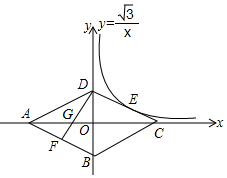 ��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������
��֪��ͼ������ABCD���ĸ���������������ϣ��Խ���AC��BD����ԭ��O��DF��AB��AC�ڵ�G������������y=$\frac{\sqrt{3}}{x}$��x��0�������߶�DC���е�E����BD=4����AG�ij�Ϊ��������| A�� | $\frac{4\sqrt{3}}{3}$ | B�� | $\sqrt{3}$+2 | C�� | 2$\sqrt{3}$+1 | D�� | $\frac{3\sqrt{3}}{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������
��ͼ��һ��ľ��AB�ij�Ϊ2mб��������洹ֱ��ǽ�ϣ���������б�ǡ�ABOΪ60�㣬��ľ����ǽ�����»�����A�䣬AA��=$\sqrt{3}-\sqrt{2}$��B���ص������һ�������B�䣬��ľ���е��P��֮�˶���P����������·����Ϊ��������| A�� | 1 | B�� | $\sqrt{3}$ | C�� | $\frac{��}{6}$ | D�� | $\frac{��}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| +2 | -3 | 0 | +4 | +6 | -6 | 0 | +3 | 4 | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5�� | B�� | 4�� | C�� | 3�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com