
���� ��1��ֱ�Ӹ��ݸ��ʹ�ʽ���㣻
��2�����������ѡ��ֱ�ΪA��B��C��D��E������A��BΪ��ȷѡ����б�չʾ����20�ֵȿ��ܵĽ�������ҳ�AB��ռ�������Ȼ����ݸ��ʹ�ʽ��⣻
��3����ֻѡȷ�ϵ���һ����ȷ�𰸿ɵ�2�֣��ټ������ѡ��ȷ�ϵ���һ����ȷ�𰸣�������ѡ��ʣ�µ��ĸ�ѡ���е�һ�����õķ�����Ȼ��Ƚ������ĵ÷ֺ�ȷ����Ѵ�����ԣ�
��� �⣺��1�����ѡ������������ȷ�𰸣���ѡһ���𰸣�ѡ����ȷ�𰸵ĸ���=$\frac{2}{5}$��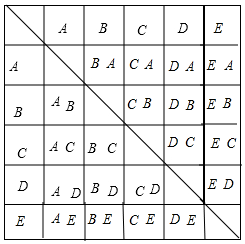
��2�����������ѡ��ֱ�ΪA��B��C��D��E������A��BΪ��ȷѡ��
�б����£�
����20�ֵȿ��ܵĽ����������ABռ2���������
���Ե�4�ֵĸ���=$\frac{2}{20}$=$\frac{1}{10}$��
��3��ֻѡȷ�ϵ���һ����ȷ�𰸣���ɵ�2�֣�
������ѡ��ȷ�ϵ���ȷ��A���ٴ�B��C��D��E������ѡ��ʣ�µ��ĸ�ѡ���е�һ����
����ѡ��ȷ�𰸵ĸ���Ϊ$\frac{1}{4}$��ѡ����𰸵ĸ���Ϊ$\frac{3}{4}$��
���Դ�ʱ�÷�=4��$\frac{1}{4}$+0��$\frac{3}{4}$=1��
���Դ�ʱ����Ѵ��������ֻѡȷ�ϵ���һ����ȷ�𰸣�
�ʴ�ΪA��
���� ���⿼�����б�������״ͼ���������б�������״ͼչʾ���п��ܵĽ�����n���ٴ���ѡ�������¼�A��B�Ľ����Ŀm��Ȼ����ݸ��ʹ�ʽ�����¼�A��B�ĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
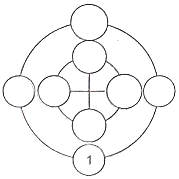 ��2��3��4��5��6��7��8���߸����ֱ�����ͼ�е��߸�СԲ�У�ʹ�ᡢ�����ڡ�������ԲȦ�ϵ�4����֮�Ͷ���ȣ�
��2��3��4��5��6��7��8���߸����ֱ�����ͼ�е��߸�СԲ�У�ʹ�ᡢ�����ڡ�������ԲȦ�ϵ�4����֮�Ͷ���ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | |-6| | B�� | ��-6��2 | C�� | ��-6��3 | D�� | -��-6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��-5 | B�� | 1��-1 | C�� | 5��1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪P�ǵȱߡ�ABC��һ�㣬��PA=3��PB=5��PC=4�����ABC�����=$\frac{36+25\sqrt{3}}{4}$��
��֪P�ǵȱߡ�ABC��һ�㣬��PA=3��PB=5��PC=4�����ABC�����=$\frac{36+25\sqrt{3}}{4}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com