
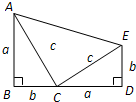
 伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.
伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
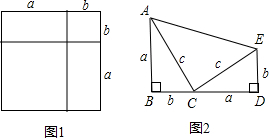 公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.
公式和图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)如图1是一个重要公式的几何解释,请你写出这个公式
(1)如图1是一个重要公式的几何解释,请你写出这个公式查看答案和解析>>
科目:初中数学 来源: 题型:
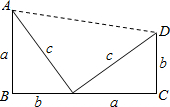 (2010•南浔区模拟)利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为
(2010•南浔区模拟)利用图中图形的有关面积的等量关系都能证明数学中一个十分著名的定理,此证明方法就是美国第二十任总统伽菲尔德最先完成的,人们为了纪念他,把这一证法称为“总统”证法.这个定理称为查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |

| 12 |
| 5 |
| 12 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com