
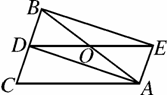
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
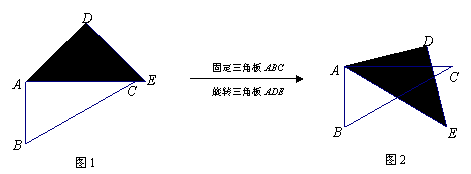
如图1,将三角板ABC与三角板ADE摆放在一起;如图2,其中∠ACB=30°,∠DAE=45°∠BAC=∠D =90°.固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时, AD∥ BC,并在图3中画出相应的图形;
BC,并在图3中画出相应的图形;
(2)当△ADE 的一边与 △ABC的某一边平行(不共线)时,写出旋转角 α的所有可能的度数;
△ABC的某一边平行(不共线)时,写出旋转角 α的所有可能的度数;
(3)当0°<α<45°时,连结BD,利用图4探究∠BDE+∠CAE+ ∠DBC值的大小变化情况,并给出你的证明.
∠DBC值的大小变化情况,并给出你的证明.
 |

 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
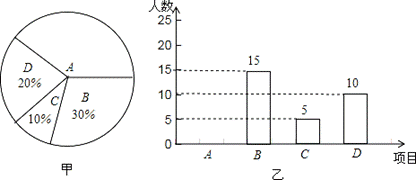
(1)样本中最喜欢A项目的人数所占的百分比为 ,其所在扇形统计图中对应的圆心角
度数是 度;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com