
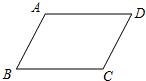
 17、如图,请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°中,选出两个,推出四边形ABCD是平行四边形:
17、如图,请在下列四个条件:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°中,选出两个,推出四边形ABCD是平行四边形:

科目:初中数学 来源: 题型:
 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).查看答案和解析>>
科目:初中数学 来源: 题型:
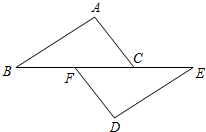 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列四个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列四个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.查看答案和解析>>
科目:初中数学 来源:新教材完全解读 七年级数学 (下册) (配人教版新课标) (第1次修订版) 配人教版新课标 题型:044
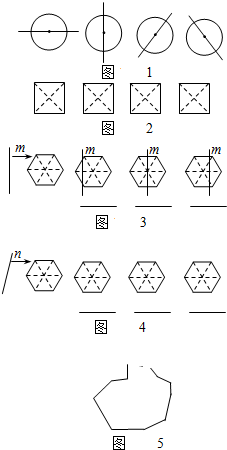
图形的操作过程如图所示(本题中四个矩形水平方向的长均为a,竖直方向的长均为b):

在图①中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分).
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
请回答下列问题:
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请分别写出上述三个图形中除去阴影部分的剩余部分的面积:
S1=________;S2=________;S3=________;
(3)联想与探索:
如图④所示,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列四个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明. 供选择的四个条件(请从其中选择一个):
①AB=ED; ②![]() ;
;
③∠ACB=∠DFE;④![]() .
.
 |
查看答案和解析>>
科目:初中数学 来源:2013年安徽省池州市中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com