Question

（12分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D.

求证：（1）△CDE是等腰三角形；
（2）△BEC∽△ADC；
（3）.

Answer 1

证明：（1）∵AB＝AC，∴∠ABC＝∠C，∵四边形ABDE是圆内接四边形，∴∠CED＝∠ABC，∴∠C＝∠CED，∴DE＝CD,即△CDE是等腰三角形；
（2）∵∠CBE与∠CAD是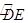所对的圆周角，∴∠CBE＝∠CAD，又∵∠BCE＝∠ACD，∴△BEC∽△ADC；
（3）由△BEC∽△ADC，知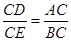，即CD•BC＝AC•CE，∵AB是⊙O的直径，∴∠ADB＝90°，即AD是底边BC上的高，又∵AB＝AC，∴△ABC是等腰三角形，∴D是BC的中点；∴CD＝BC，又∵AB＝AC，∴CD•BC＝AC•CE＝BC•BC＝AB•CE，即BC²＝2AB•CE．

解析（1）先根据AB＝AC，得出∠ABC＝∠C，再由圆内接四边形的性质得出∠CED＝∠ABC，故可得出∠C＝∠CED，由此可得出结论；（2） 欲证△BEC∽△ADC，通过观察发现两个三角形已经具备一组角对应相等，即∠AEB＝∠ADC＝90°，此时，再求另一角对应相等即可；（3）由△BEC∽△ADC可证CD•BC＝AC•CE，又D是BC的中点，AB＝AC，即可证BC²＝2AB•CE．
考点：等腰三角形的判定与性质；圆周角定理；相似三角形的判定与性质．
点评：本题考查相似三角形的判定和性质．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边成比例、对应角相等．