
 如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO.
如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO.| 1 |
| 2 |
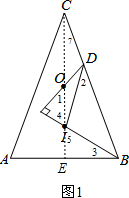
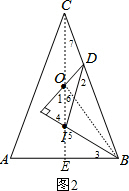
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 3 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
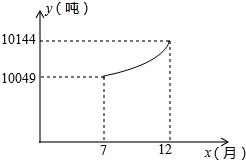 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年下半年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.7至12月,该企业自身处理的污水量y(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为y=ax2+c(a≠0),其图象如图所示.污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.| 231 |
| 419 |
| 809 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
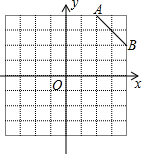 如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题:
如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 数 | 第1组 | 第2组 | 第3组 | 第4组 | 第5组 | 第6组 | … |
| a | 5 | -5 | 6 | -6 | -10 | -2.5 | … |
| b | 3 | 0 | -4 | -4 | 2 | -2.5 | … |
| A,B两点的距离 | 2 | 0 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com