
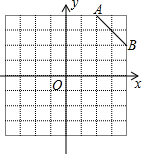
 如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题:
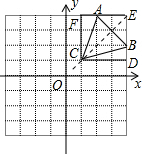
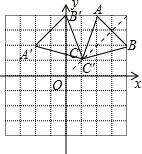
如图在8×8的正方形网格中建立直角坐标系,已 知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形,画出图形,并解答下列问题: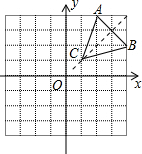 ,
,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 ,
,| 2 |
270×π×2
| ||
| 180 |
| 2 |


科目:初中数学 来源: 题型:
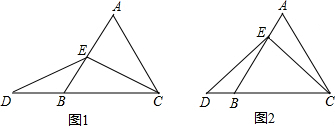
查看答案和解析>>
科目:初中数学 来源: 题型:
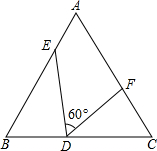 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发,设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程始终保持∠EDF=60°.| 9 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
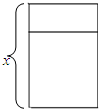 某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).
某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
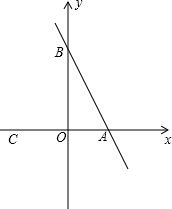 已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D.
已知在平面直角坐标系中,点A、B的坐标分别为A(3,0)、B(O,4),点C的坐标为C(-2,O),点P是直线AB上的一动点,直线CP与y轴交于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com