练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图是一个矩形的储物柜，它被分成4个大小不同的正方形①②③④和一个矩形⑤，若要计算⑤的周长，则只需要知道哪个小正方形的周长？你的选择是（　　）
    A．①B．②C．③D．④

    分析 记正方形①②③④的边长分别为a、b、c、d．则矩形的周长=2[d+a+（b-a））]，由c=a+b=d-a等量代换即可解决问题．

    解答 解：记正方形①②③④的边长分别为a、b、c、d．
    则矩形⑤的周长=2[d+a+（b-a））]，
    因为c=a+b=d-a，
    所以矩形⑤的周长=2[d+a+（b-a））]=2[（d-a）+（a+b）]=2（2a+2b）=4（a+b）=4c．
    所以只要知道③的边长即可计算⑤的周长．
    故选C．

    点评 本题考查矩形的性质、周长等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．在有理数的原有运算法则中我们补充定义新运算“?”如下：当a≥b时，a?b=a2；当a＜b时，a?b=b，则当x=2时，（1?x）?x-（3?x）的值为-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若sinα•cosα=$\frac{1}{8}$，且45°＜α＜90°，则cosα-sinα的值为-$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．在钟盘上时针和分针恰好互相垂直，并且此时表示的时间恰好是整点的时间有3或9；一天24小时，时针与分针互相垂直44次；从2点整开始，分针经过$\frac{300}{11}$分钟第一次与时针垂直；从5点整开始，分针经过$\frac{120}{11}$分钟第一次与时针垂直．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

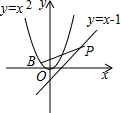    16．如图，点P在直线y=x-1上，若存在过点P的直线交抛物线y=x2于A、B两点，且PA=AB，则称点P为“优点”，下列结论中正确的是（　　）
    A．直线y=x-1上的所有点都是“优点”
    B．直线y=x-1上仅有有限个点是“优点”
    C．直线y=x-1上的所有点都不是“优点”
    D．直线y=x-1上有无穷多个点（不是所有的点）是“优点”

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知三角形的第一条边长是a+2b，第二边长比第一条边长大（b-2），第三条边长比第二条边小5，求三角形的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知如图所示△ABC中，∠ACB=90°，AC=BC，点P在△ABC内，且PA=$\sqrt{3}$，PB=1，PC=1，则∠BPC=135°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．设a≠0，x，y是正整数，定义新运算a⊕x=ax（如果有括号，规定先算括号里面的）如：2⊕2=22=4，4⊕（m+1）=4m+1
    （1）若10⊕n=100，则n=2；
    （2）请你证明：（a⊕x）（a⊕y）=a⊕（x+y）；
    （3）若（2⊕x）（2⊕2y）=8且（3⊕x）（3⊕y）=9，请运用（2）中的结论求x、y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，BC=10$\sqrt{3}$，试求CD的长．

    查看答案和解析>>

    同步练习册答案