
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:





查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
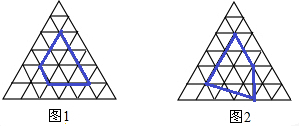
| 格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1 | 8 | 1 | |
| 多边形2 | 7 | 3 | |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则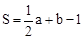 (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
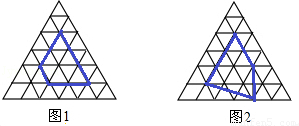
根据图中提供的信息填表:
|
|
格点多边形各边上的格点的个数 |
格点边多边形内部的格点个数 |
格点多边形的面积 |
|
多边形1 |
8 |
1 |
|
|
多边形2 |
7 |
3 |
|
|
… |
… |
… |
… |
|
一般格点多边形 |
a |
b |
S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com