练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，求证：(1)∠BDC＞∠A；

    (2)∠BDC＝∠B＋∠C＋∠A．

    如果点D在线段BC的另一侧，结论会怎样？

    答案：略
    解析：

    (1)证明：连结AD，并延长到E．

    ∵∠EDC、∠EDB分别为△ADC、△ADB的外角，

    ∴∠EDC＞∠EAC．∠EDB＞∠EAB．

    ∴∠EDC＋∠EDB＞∠EAC＋∠EAB

    即∠BDC＞∠BAC．

    (2)延长BD交AC于E点，则∠BDC＋∠CDE＝180°，

    ∴∠BDC＝180°－∠CDE．

    ∵∠DEC为△ABE的外角，

    ∴∠DEC＝∠A＋∠B．

    又∵∠C＋∠CDE＋∠DEC＝180°，

    ∴∠C＋∠CDE＋∠A＋∠B＝180°．

    ∴∠A＋∠B＋∠C＝180°－∠CDE．

    ∴∠BDC＝∠A＋∠B＋∠C．

    当D在线段BC的另一侧时，则∠BDC＝360°－(∠B＋∠C＋∠A)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

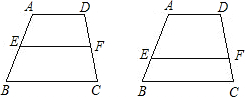    精英家教网已知：在梯形ABCD中，AD∥BC，点E在AB上，点F在DC上，且AD=a，BC=b．
    （1）如果点E、F分别为AB、DC的中点，如图．求证：EF∥BC，且EF=
    a+b
    2
    ；
    （2）如果
    AE
    EB
    =
    DF
    EC
    =
    m
    n
    ，如图，判断EF和BC是否平等，并用a、b、m、n的代数式表示EF．请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：⊙O1与⊙O2相交于点A、B，过点B作CD⊥AB，分别交⊙O1和⊙O2于点C、D．
    （1）如图，求证：AC是⊙O1的直径；
    （2）若AC=AD，
    ①如图，连接BO2、O1O2，求证：四边形O1C BO2是平行四边形；
    ②若点O1在⊙O2外，延长O2O1交⊙O1于点M，在劣弧
    MB
    上任取一点E（点E与点B不重合），EB的延长线交优弧
    BDA
    于点F，如图所示，连接AE、AF，则AE
     
    AB（请在横线上填上“≥、≤、＜、＞”这四个不等号中的一个）并加以证明．（友情提示：结论要填在答题卡相应的位置上）
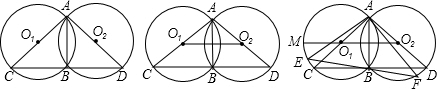
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

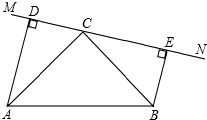    如图，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN，垂足为D，BE精英家教网⊥MN，垂足为E
    （1）如图，求证：DE=AD+BE；
    （2）保持上述条件不变，若直线MN绕点C进行旋转，使MN经过△ABC的内部，则DE，AD，BE具有怎样的等量关系？请画出草图并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    24、已知：如图，求证：∠1-∠2=∠A-∠B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    等边△ABC中，点D在BC上，点E在AB上，且CD=BE，以AD为边作等边△ADF，如图．求证：四边形CDFE是平行四边形．

    查看答案和解析>>

    同步练习册答案