Question

如图，A、E、F、C四点在同一直线l上，AC=8，AE=CF=1，过E、F分别作DE⊥AC，BF⊥AC，且DE=BF，连接AD、BC，连接BD交AC于点O，
（1）请直接判断AD、BC的关系．
（2）试说明O为AC的中点．
（3）若△BFC固定不动，将△ADE沿直线l平移到△A′D′E′（A、D、E的对应点分别为A′、D′、E′），连接BD′交直线l于点O′，试探究如何平移△ADE，使得OO′=1.2？请直接写出△ADE的平移方向和距离．

Answer 1

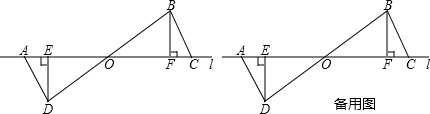
解：（1）∵DE⊥AC，BF⊥AC，
∴∠AED=∠CFB=90°，
在△ADE和△BCF中，，
∴△ADE≌△BCF（SAS），
∴AD=BC，∠DAE=∠BCF，
∴AD∥BC，
∴AD、BC平行且相等；

（2）在△ADO和△BCO中，，
∴△ADO≌△BCO（AAS），
∴AO=CO，
即O为AC的中点；

（3）∵OO′=1.2，
∴①△ADE沿直线向右平移2.4个单位，
②△ADE沿直线向左平移2.4个单位．
分析：（1）根据“边角边”证明△ADE和△BCF全等，根据全等三角形对应边相等可得AD=BC，全等三角形对应角相等可得∠DAE=∠BCF，再根据内错角相等，两直线平行即可得解；
（2）利用“角角边”证明△ADO和△BCO全等，根据全等三角形对应边相等可得AO=CO，从而得解；
（3）根据对称性，点AC间的距离的变化等于点O的变化的2倍，再分点O向右与向左两种情况解答．
点评：本题考查了平移的性质，全等三角形的判定与性质，证明三角形全等是解题的关键．