
分析 (1)把分子与分母同时乘以100即可得出结论;
(2)先找出各式分子与分母的分母的公因式,再根据分式的基本性质进行解答即可;
(3)先找出各式分子与分母的分母的公因式,再根据分式的基本性质进行解答即可;.
解答 解:(1)分式的分子与分母同时乘以100得,$\frac{0.02-0.2x}{0.3x-0.03}$=$\frac{2-20x}{30x-3}$;
(2)分式的分子与分母同时乘以6得,$\frac{\frac{1}{2}x-\frac{1}{3}y}{\frac{2}{3}x-\frac{1}{2}y}$=$\frac{3x-2y}{4x-3y}$
(3)分式的分子与分母同时乘以60得,$\frac{0.2x-\frac{1}{2}y}{\frac{1}{4}x-\frac{2}{3}y}$=$\frac{12x-30y}{15x-40y}$.
点评 本题考查的是分式的基本性质,即分式的分子与分母同乘(或除以)一个不等于0的数(或整式),分式的值不变.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
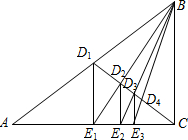 如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )
如图,已知Rt△ABC的面积为1,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn等于( )| A. | $\frac{1}{(n+1)^{2}}$ | B. | $\frac{1}{(2n)^{2}}$ | C. | $\frac{1}{4n}$ | D. | $\frac{1}{{2}^{n+1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正多边形的外接圆的圆心,就是它的中心 | |
| B. | 正多边形的外接圆的半径,就是它的半径 | |
| C. | 正多边形的内切圆的半径,就是它的边心距 | |
| D. | 正多边形的外接圆的圆心角,就是它的中心角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com