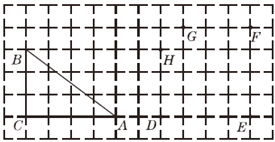
【题目】如图所示，在方格纸中，△ABC的三个顶点及D，E，F，G，H五个点分别位于小正方形的顶点上.
（1）现以D，E，F，G，H中的三个点为顶点画三角形，在所画的三角形中与△ABC不全等但面积相等的三角形是 （只需要填一个三角形）；
（2）先从D，E两个点中任意取一个点，再从F，G，H三个点中任意取两个不同的点，以所取的这三个点为顶点画三角形，画树状图求所画三角形与△ABC面积相等的概率.
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案科目：初中数学 来源： 题型：
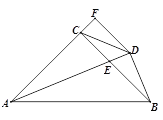
【题目】如图，在△ABC中，AC＝BC，∠ ACB＝90°，AE平分∠BAC交BC于E，BD⊥AE于D，DF⊥AC交AC的延长线于F，连接CD，给出四个结论：①∠ADC＝45°；②BD＝
AE；③AC＋CE＝AB；④AB—BC＝2FC；其中正确的结论有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
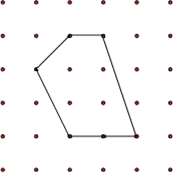
【题目】各顶点都在方格纸格点（横竖格子线的交错点）上的多边形称为格点多边形．如何计算它的面积？奥地利数学家皮克（GPick，1859～1942年）证明了格点多边形的面积公式S=a+
b﹣1，其中a表示多边形内部的格点数，b表示多边形边界上的格点数，S表示多边形的面积．如图，a=4，b=6，S=4+
×6﹣1=6
（1）请在图中画一个格点正方形，使它的内部只含有4个格点，并写出它的面积．
（2）请在图乙中画一个格点三角形，使它的面积为
，且每条边上除顶点外无其它格点．（注：图甲、图乙在答题纸上）
查看答案和解析>>
科目：初中数学 来源： 题型：
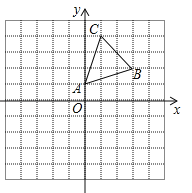
【题目】如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．
（1）画出△ABC关于x轴的对称图形△A1B1C1；
（2）将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学问题：计算
（其中m，n都是正整数，且m≥2，n≥1）．
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
．
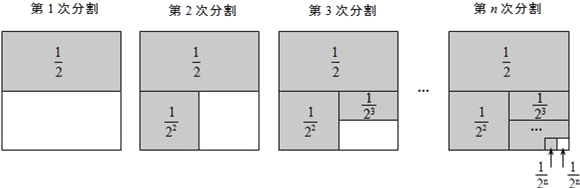
第1次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
．
探究二：计算
．
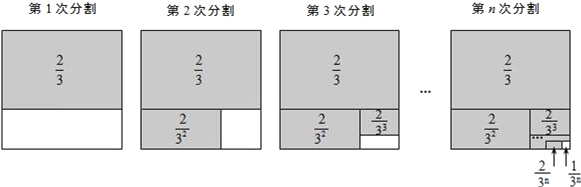
第1次分割，把正方形的面积三等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
，
两边同除以2，得
=
.
探究三：计算
．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
．
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以， 
= ．
拓广应用：计算
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
