
����Ŀ����ͼ1���ڳ�����![]() �У�
�У�![]() ����һֻ����
����һֻ����![]() �ڵ�
�ڵ�![]() ����ʼ��ÿ��1����λ���ٶ���
����ʼ��ÿ��1����λ���ٶ���![]() �����
�����![]() ���У���һֻ����
���У���һֻ����![]() �ӵ�
�ӵ�![]() ��ÿ��2����λ���ٶ���
��ÿ��2����λ���ٶ���![]() �����
�����![]() ���У����ϵĴ�С���Բ��ƣ����
���У����ϵĴ�С���Բ��ƣ����![]() ��
��![]() ͬʱ���������˶�ʱ��Ϊ
ͬʱ���������˶�ʱ��Ϊ![]() s.
s.

(1)��![]() ʱ����
ʱ����![]() �����;
�����;
(2)��![]() ʱ����˵��
ʱ����˵��![]() ��ֱ�Ƕ�����;
��ֱ�Ƕ�����;
(3)���˶�3sʱ��![]() ��ֹͣ�˶���
��ֹͣ�˶���![]() ����ԭ��������
����ԭ��������![]() �㷵�أ��ڷ��صĹ����У��Ƿ���ڵ�
�㷵�أ��ڷ��صĹ����У��Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ?�����ڣ������
?�����ڣ������![]() �˶���ʱ�䣬����������˵������.
�˶���ʱ�䣬����������˵������.
���𰸡���1��8����2�������������3�����ڵ�Q��ʹ��DPƽ��![]() ����ʱ
����ʱ![]() s
s
��������
��1�������������t=2ʱPB��BQ�ij���Ȼ����������������ʽ������������
��2�����ù��ɶ������DP��PQ��DQ���õ�![]() ����֤����
����֤����
��3����������õ�AP=3����Q���˶�x�룬��x��ʾ��BQ��CQ����PH��BC��H����֤![]() �����DQ�������Rt��DCQ�����ù��ɶ����������̽��x��Ȼ�����3�룬��ΪQ���˶�ʱ��.
�����DQ�������Rt��DCQ�����ù��ɶ����������̽��x��Ȼ�����3�룬��ΪQ���˶�ʱ��.
��1����![]() ʱ��
ʱ��![]()
![]() S��ABD =
S��ABD =![]() ��4��4=8
��4��4=8
��2����![]() ʱ��
ʱ��![]()
��![]()
![]()
![]()
��![]()
�ߡ�DQP=90��,
��![]() ��ֱ��������.
��ֱ��������.

(3) ��![]() ʱ��
ʱ��![]() ����P��AB���е㣬PA=PB=3��
����P��AB���е㣬PA=PB=3��
��ʱBQ=6�����Q����ʱ���˶�x�����Ҫ����
![]()
��PH��BC��H����PDƽ�֡�ADQ���֡�PA��AD��
![]()
��Rt��PBQ��Rt��PHQ��PQ=PQ��PB=PH��
![]() ��
��
![]()
��Rt��DCQ��![]()
![]() ���
���![]()
����Q���˶�ʱ��Ϊ![]() ��
��
�𣺴��ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ����ʱQ���˶�ʱ��Ϊ
����ʱQ���˶�ʱ��Ϊ![]() ��.
��.


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����|x��3|+��4+y��2+![]() =0����3x+y+z��ֵ��
=0����3x+y+z��ֵ��
��2����2+![]() ��С��������a����a��a+2����ֵ��
��С��������a����a��a+2����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˶�ѧ�����а������������ijУ��֯ѧ��ȥ���ݳ����м�������Ʊ����֪��������Ʊ�ĵ��۱�Ϊ4��3�����ۺ�Ϊ42Ԫ.
��1����������Ʊ�ĵ��۷ֱ��Ƕ���Ԫ��
��2��ѧУ�ƻ��ó�������750Ԫ���ʽ������꼶һ���36��ѧ�����ȹۿ����ҹ涨�������Ʊ�������15�ţ����ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
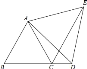
����Ŀ����ͼ����֪�ȱߡ�ABC�У���D��BC�ߵ��ӳ����ϣ�CEƽ�֡�ACD����CE=BD.�жϡ�ADE����״����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�⣺
��ͼ����10��10�������������У�ÿ��С�����εı߳���Ϊ1����������һ�������ABC���������εĶ��㶼�ڸ���ϣ���

��1����ͼ�л�����ABC����ֱ��l�ԳƵ���A1B1C1��
��Ҫ��A��A1��B��B1��C��C1���Ӧ��
��2�������A1B1C1�����
��3����ֱ��l����һ��P��ʹ��PA+PB��ֵ��С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
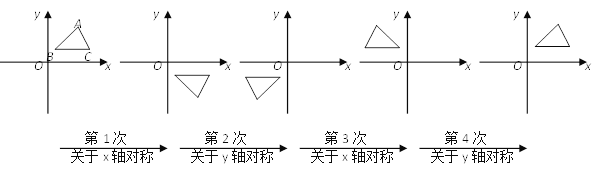
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ԡ�ABC����ѭ����������ԳƱ任����ԭ����A�����ǣ�2��3��������2018�α任�����õ�A��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Գ���Ϊy���������y=ax2+bx+3����x����������ĺ�����ֱ�Ϊx1��x2�����㣨x1��x2���ڷ���������y=![]() ��ͼ���ϣ�����������x��Χ�ɷ�����߽���⣩�����㣨��ĺᡢ�����궼���������ĸ���Ϊk����������y=
��ͼ���ϣ�����������x��Χ�ɷ�����߽���⣩�����㣨��ĺᡢ�����궼���������ĸ���Ϊk����������y=![]() ��x��0����ͼ���ǣ�������
��x��0����ͼ���ǣ�������
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P�ǡ�AOB���ڲ�����һ�㣬PM��OA��PN��OB������ֱ���M��N��D��OP���е�
��1����֤��DM=DN
��2������MN,����MPN=______ʱ����DMN�ǵȱ������Σ�
��3��̽����MPN���MDN��������ϵ����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ1����ABC����DCE���ǵȱ������Σ���B��D��E��ͬһֱ���ϣ�����AE��
��գ�
�١�AEC�Ķ���Ϊ�� ����
���߶�AE��BD֮���������ϵΪ�� ����
��2����չ̽��
��ͼ2����ABC����DCE���ǵ���ֱ�������Σ���ACB=��DCE=90�㣬��B��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����AE��������AEB�Ķ������ж��߶�CM��AE��BM֮���������ϵ����˵�����ɣ�
��3���������
��ͼ3����������ABCD�У�CD=2����P����ACΪֱ���İ�Բ�ϣ�AP=1���١�DPC=�� �㣻 ����ֱ��д����D��PC�ľ���Ϊ�� ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com