
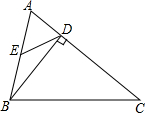
 如图,在锐角△ABC中,点E为AB的中点,BD⊥AC于点D,若AC=20,CD=15,tanC=
如图,在锐角△ABC中,点E为AB的中点,BD⊥AC于点D,若AC=20,CD=15,tanC=| 4 |
| 5 |
| AD2+BD2 |
| BD |
| AB |
| 12 |
| 13 |
| BD |
| AB |
| 12 |
| 13 |
| BD |
| CD |
| BD |
| 15 |
| 4 |
| 5 |
| AD2+BD2 |
| 52+122 |
| 1 |
| 2 |
| BD |
| AB |
| 12 |
| 13 |
| BD |
| AB |
| 12 |
| 13 |
| 12 |
| 13 |


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
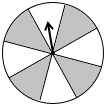 有一个能自由转动的转盘如图,盘面被分成8个大小与性状都相同的扇形,颜色分为黑白两种,将指针的位置固定,让转盘自由转动,当它停止后,指针指向白色扇形的概率是
有一个能自由转动的转盘如图,盘面被分成8个大小与性状都相同的扇形,颜色分为黑白两种,将指针的位置固定,让转盘自由转动,当它停止后,指针指向白色扇形的概率是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.
如图,四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F,垂足分别为E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com