
 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).
如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6). 分析 根据轴对称的性质可得OB=OB′,设C′(2,y),再把AC′的值代入直线y=x+b即可得出y的值,进而得出点C′的坐标即可.
解答 解:∵A(-4,0),B(-2,0),
∴AO=4,OB=2,
∵△A′B′C′和△ABC关于y轴对称,
∴OB=OB′=2,
∴B′(2,y)
∵直线y=x+b经过点A,C′,
∴$\left\{\begin{array}{l}{2+b=y}\\{-4+b=0}\end{array}\right.$,
∴点C′的坐标为(2,6).
故答案为:(2,6)
点评 本题考查了一次函数图象上点的坐标特征,坐标与图形变化-对称,根据直线解析式的k值等于1得到AB′=B′C′是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
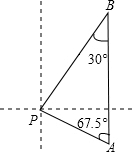 在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)
在一次海事活动中,我“海巡01号”轮船上午9时位于海面上的A处,观测到某小岛P位于它的北偏西67.5°方向上,该船以21海里/时的速度向正北方向行驶,下午2时到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(结果精确到0.1,参考数据:sin67.5°=$\frac{12}{13}$,cos67.5°=$\frac{5}{13}$,tan67.5°=$\frac{12}{5}$,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
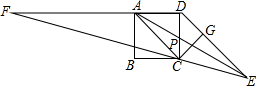 如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )
如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com