
����Ŀ����ͼ��ADΪ��O��ֱ��������O���ڽ���������ABC���ס������˵������ֱ��ǣ� �ף��١���OD���д��ߣ�����O��B��C���㣬
�ڡ�����AB��AC����ABC��Ϊ�����������
�ң��١���DΪԲ�ģ�OD��Ϊ�뾶��Բ��������O��B��C���㣮
�ڡ�����AB��BC��CA����ABC��Ϊ����������Σ�
���ڼס������˵����������жϣ� ��
A.�ס��Ҿ���ȷ
B.�ס��Ҿ�����
C.����ȷ���Ҵ���
D.�״�������ȷ
���𰸡�A
���������⣺���ݼ�˼·������ͼ�����£� 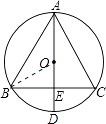
����OB��
��BC��ֱƽ��OD��
��EΪOD���е㣬��OD��BC��
��OE=DE= ![]() OD����OB=OD��
OD����OB=OD��
��Rt��OBE��OE= ![]() OB��
OB��
���OBE=30�㣬�֡�OEB=90�㣬
���BOE=60�㣬
��OA=OB�����OAB=��OBA��
�֡�BOEΪ��AOB����ǣ�
���OAB=��OBA=30�㣬
���ABC=��ABO+��OBE=60�㣬
ͬ����C=60�㣬
���BAC=60�㣬
���ABC=��BAC=��C��
���ABCΪ�ȱ������Σ�
�ʼ�������ȷ��
�����ҵ�˼·����ͼ���£�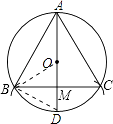
����OB��BD��
��OD=BD��OD=OB��
��OD=BD=OB��
���BODΪ�ȱ������Σ�
���OBD=��BOD=60�㣬
��BC��ֱƽ��OD����OM=DM��
��BMΪ��OBD��ƽ���ߣ�
���OBM=��DBM=30�㣬
��OA=OB���ҡ�BODΪ��AOB����ǣ�
���BAO=��ABO=30�㣬
���ABC=��ABO+��OBM=60�㣬
ͬ����ACB=60�㣬
���BAC=60�㣬
���ABC=��ACB=��BAC��
���ABCΪ�ȱ������Σ�
����������ȷ��
��ѡA
�����㾫����������Ĺؼ��������⺬30�Ƚǵ�ֱ�������ε����֪ʶ��������ֱ���������У����һ����ǵ���30�㣬��ô�����Ե�ֱ�DZߵ���б�ߵ�һ�룬�Լ��Դ������������⣬�˽ⴹ��������ƽ���ң�����ֱ������ֱ����ֱ���ң�����ƽ�������Ե���������


 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ����������������塱��У���Ҵ�峤��������ֹ�������Ͱ����������1�����������Ͱ����Ҫ����3000Ԫ���Ժ�ÿ�µ�������������250Ԫ������2����������Ͱ����Ҫ����1000Ԫ���Ժ�ÿ�µ�������������500Ԫ���跽��1�Ĺ���Ѻ�ÿ�����������ѹ�Ϊy1Ԫ������ʱ��Ϊx���£�����2�Ĺ���Ѻ�ÿ�����������ѹ�Ϊy2Ԫ������ʱ��Ϊx���£�
��1��ֱ��д��y1��y2��x�ĺ�����ϵʽ��
��2����ͬһ����ϵ�ڣ���������y1��y2��ͼ��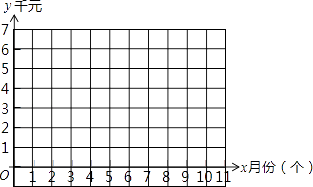
��3��������Ͱʹ��������ͬ������£����ַ���ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
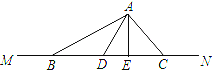
����Ŀ����ͼ��MN��һ����������ı�ֱ�Ĺ�·��C��λ�ڸù�·�ϵ�һ����������Ϊ9m��С����BD��ʻ�ڸù�·��С��λ�ڵ�A���۲�С������ijʱ�������ֳ�ͷD����βB������C�ֱ������10m��17m��2![]() m
m
��1������A��MN�����ߣ�����ΪE�������ù��ɶ����ֱ��ҳ��߶�AE��DE��AE��BE֮���������������ϵ��
��2������һ�ʵ���ʾ�£���������������⣺
�����߶�DE�ij��ȣ�
����С�����ij�ͷD�������C���ж���m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬D�DZ�AB��һ�㣬�ҡ�A=2��DCB��E��BC���ϵ�һ�㣬��ECΪֱ���ġ�O������D�� 
��1����֤��AB�ǡ�O�����ߣ�
��2����CD�����ľ�Ϊ1��BE=EO����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�ᳫ��Լ��ˮ����ʵ������ˮ�����ݼƷѡ���ʽ���û���ˮ������������ˮ���IJ������ܻ����۸���������ˮ���IJ���ʵ�мӼ��շѣ�Ϊ���õؾ��ߣ�����ˮ��˾�����ȡ�����û�����ˮ�����ݣ������������²�����ͳ��ͼ��ÿ�����ݰ����Ҷ˵㵫��������˵㣩���������ͳ��ͼ����������⣺ 
��1���˴ε����ȡ�˶����û�����ˮ�����ݣ�
��2����ȫƵ���ֲ�ֱ��ͼ��������ͳ��ͼ�С�25�֡�30�֡����ֵ�Բ�ĽǶ�����
��3���������ˮ��˾��������ˮ����Ϊÿ��25�֣���ô�õ�20���û���Լ�ж����û�����ˮȫ�����ܻ����۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�����������������ϣ�OA=1��OC=2���ֽ��˾�������ƽ�ƣ�ÿ��ƽ��1����λ������1��ƽ�Ƶõ��ľ��εı��뷴��������ͼ�����������㣬���ǵ�������֮��ľ���ֵΪ0.6�����n�Σ�n��1��ƽ�Ƶõ��ľ��εı���÷���������ͼ������������������֮��ľ���ֵΪ���ú�n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Խ��Ƶؿ̻������ĸ��龰(����)
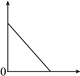
A. С�����ٲ�����ѧʱ��ѧУ�ľ�����ʱ��Ĺ�ϵ
B. ������ʻ���������ٶ���ʱ��Ĺ�ϵ
C. С�����赽���й���ƻ�����ܷ�����ƻ�������Ĺ�ϵ
D. һ����������������ĸ߶���ʱ��Ĺ�ϵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1��x2�Ƿ���x2��5x��6=0���������������ʽx12+x22��ֵ�ǣ� ��
A.37
B.26
C.13
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
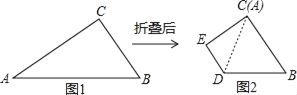
����Ŀ����ͼ�٣���ABC�У���ACB��90�㣬AC��3![]() ��BC��3����ͼ��������ABC��һ��ֱ���۵���ʹ�õ�A���C�غ�
��BC��3����ͼ��������ABC��һ��ֱ���۵���ʹ�õ�A���C�غ�
(1)��ͼ���л����ۺ����ڵ�ֱ��l����ֱ��l��AB��AC�ֱ��ཻ�ڵ�D��E(�߹���ͼ����д������������ͼ�ۼ�)
(2)��ͼ�������CDB���ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com