
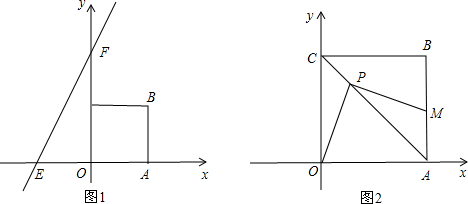
���� ��1�������߶ε��е���������⣮
��2��E�������Ϊ��-4��0������ֱ��EFƽ�Ƶ���D��ʱ����ƽ��������AOBC���������ƽ�ƺ��ֱ��Ϊy=2x+b������D�����꣬���b=-2����֪ƽ�Ƶľ���Ϊ5������t=5��
��3����P����NQ��OA��GH��CO����CO��AB��N��Q����CB��OA��G��H����֤��OPH�ա�MPQ���ı���CNPGΪ�����Σ���֪PG=BQ=CN���������$\frac{PC}{BM}=\frac{\sqrt{2}}{2}$��
��� �⣺��1������$\sqrt{a-4}$+b2-8b+16=$\sqrt{a-4}$+��b-4��2=0��
��a-4=0����b-4=0��
��a=4��b=4��
��B��������4��4����
��OA=AB=BC=CO=4��
���ı���OABC�����S=OA•AB=4��4=16��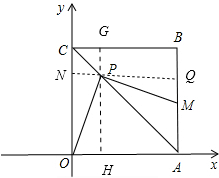 ��2����y=0ʱ��x=-4��
��2����y=0ʱ��x=-4��
��E���������-4��0����
��ֱ��EFƽ�Ƶ���D��ʱ����ƽ��������AOBC�������
��ƽ�ƺ��ֱ��Ϊy=2x+b������D�����꣬���b=-2��
��ʱֱ�ߺ�x��Ľ�������Ϊ��1��0����ƽ�Ƶľ���Ϊ5������t=5�룮
��3����P����NQ��OA��GH��CO����CO��AB��N��Q����CB��OA��G��H��
�ڡ�OPH���MPQ�У�
$\left\{\begin{array}{l}{OP=PM}\\{PH=PQ}\end{array}\right.$��
���OPH�ա�MPQ���ı���CNPGΪ�����Σ�
��PG=BQ=CN��
��$CP=\sqrt{2}PG=\frac{\sqrt{2}}{2}PM$����$\frac{PC}{BM}=\frac{\sqrt{2}}{2}$��
���� ��Ҫ�����˺����ͼ���ͼ�ε��ۺ����ã�����Ĺؼ��ǻ��������ú���ͼ������ʺͽ�������������Ӧ���߶εij��Ȼ��ʾ�߶εij��ȣ��ٽ�Ͼ���ͼ�ε�������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��PA��PB�ǡ�O�����ߣ�A��B���е㣬��C���ӻ�AB�ϵ�һ�����㣬����ACB=110�㣬���P�Ķ����ǣ�������
��ͼ��PA��PB�ǡ�O�����ߣ�A��B���е㣬��C���ӻ�AB�ϵ�һ�����㣬����ACB=110�㣬���P�Ķ����ǣ�������| A�� | 55�� | B�� | 30�� | C�� | 35�� | D�� | 40�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
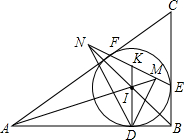 ��ͼ����ABC������ԲI�ڱ�AB��BC��CA�ϵ��е�ֱ���D��E��F��ֱ��EF��ֱ��AI��BI��DI�ֱ��ཻ�ڵ�M��N��K��
��ͼ����ABC������ԲI�ڱ�AB��BC��CA�ϵ��е�ֱ���D��E��F��ֱ��EF��ֱ��AI��BI��DI�ֱ��ཻ�ڵ�M��N��K���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
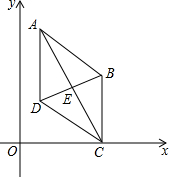 ��ͼ����ƽ��ֱ������ϵ�У���A��1��4��B��m��n����m��2����D��1��q����q��n������B��D��ֱ��y=$\frac{1}{2}$x+1�ϣ��ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�E����AB��CD����C��x���ϣ�BE=DE����֤���ı���ABCD�����Σ�
��ͼ����ƽ��ֱ������ϵ�У���A��1��4��B��m��n����m��2����D��1��q����q��n������B��D��ֱ��y=$\frac{1}{2}$x+1�ϣ��ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�E����AB��CD����C��x���ϣ�BE=DE����֤���ı���ABCD�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com