



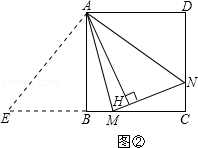
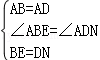 ����Rt��AEB��Rt��AND����AE=AN����EAB=��NAD�����EAM=��NAM=45�㣬�ڡ�AEM�͡�ANM�У�
����Rt��AEB��Rt��AND����AE=AN����EAB=��NAD�����EAM=��NAM=45�㣬�ڡ�AEM�͡�ANM�У�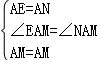 �����AEM�ա�ANM����AB��AH�ǡ�AEM�͡�ANM��Ӧ���ϵĸߣ���AB=AH��
�����AEM�ա�ANM����AB��AH�ǡ�AEM�͡�ANM��Ӧ���ϵĸߣ���AB=AH��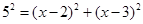 ��
��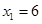 ��
��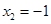 �����������⣬��ȥ������AH=6��
�����������⣬��ȥ������AH=6��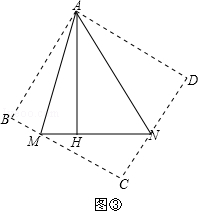



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��y�ᡢֱ��l�ֱ��ڵ�C��D�����ACD��y����תһ����Χ�ɼ�����ı������
��y�ᡢֱ��l�ֱ��ڵ�C��D�����ACD��y����תһ����Χ�ɼ�����ı������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
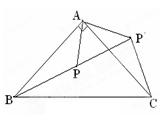
A��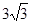 | B��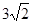 | C��5 | D��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
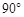 ���á�ABF������EF����EF�ij����� ��
���á�ABF������EF����EF�ij����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A���������� | B������ֱ�������� | C���������� | D�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 =�� ����
=�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com