
科目:初中数学 来源: 题型:
某制药厂两年前生产1吨某种药 品的成本是100万元,随着生产技术的进步,现在生
品的成本是100万元,随着生产技术的进步,现在生
产1吨这种药品的成本为81万元,则这种药品的成本的年平均下降率为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
关于x的方程: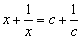 的解是
的解是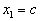 ,
,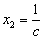 ;
;
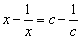 (即
(即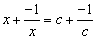 )的解是
)的解是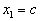
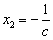 ;
;
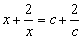 的解是
的解是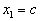 ,
,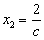 ;
;
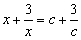 的解是
的解是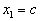 ,
, ;……
;……
(1) 请观察上述方程与解的特征,则关于于x的方程
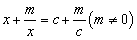 的解
的解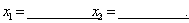
(2) 用“方程的解”的概念对(1)的解进行验证。
(3)由上述的观察、比较、猜想、验证,可以得出结论: 如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这 个结论解关于x的方程:
个结论解关于x的方程: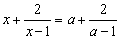 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料:
问题:在平面直角坐标系 中,一张矩形纸片
中,一张矩形纸片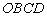 按图1所示放置。已知
按图1所示放置。已知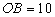 ,
,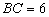 ,
,
将这张纸片折叠,使点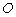 落在边
落在边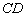 上,记作点
上,记作点 ,折痕与边
,折痕与边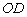 (含端点)交于点
(含端点)交于点 ,与边
,与边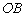 (含端
(含端
点)或其延长线交于点 ,求点
,求点 的坐标。
的坐标。
小明在解决这个问题时发现:要求点 的坐标,只要求出线段
的坐标,只要求出线段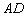 的长即可,连接
的长即可,连接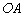 ,设折痕
,设折痕 所
所
在直线对应的函数表达式为: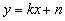
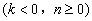 ,于是有
,于是有 ,
,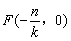 ,所以在
,所以在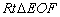
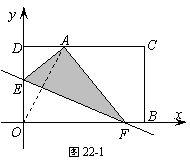 中,得到
中,得到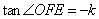 ,在
,在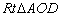 中,利用等角的三角函数值相等,就可以求出线段
中,利用等角的三角函数值相等,就可以求出线段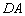 的长(如图
的长(如图
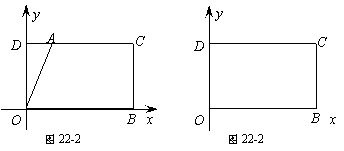 1)
1)
 |
请回答:
(1)如图1,若点 的坐标为
的坐标为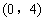 ,直接写出点
,直接写出点 的坐标;
的坐标;
(2)在图2中,已知点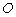 落在边
落在边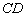 上的点
上的点 处,请画出折痕所在的直线
处,请画出折痕所在的直线 (要求:尺规作图,保留作图痕迹,不写做法);
(要求:尺规作图,保留作图痕迹,不写做法);
参考小明的做法,解决以下问题:
(3)将矩形沿直线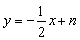 折叠,求点
折叠,求点 的坐标;
的坐标;
(4)将矩形沿直线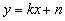 折叠,点
折叠,点 在边
在边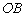 上(含端点),直接写出
上(含端点),直接写出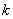 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com